早教吧作业答案频道 -->数学-->
已知方程|lnx|=kx+1在(0,e3)上有三个不等实根,则实数k的取值范围是()A.(0,2e3)B.(3e3,2e2)C.(2e3,1e2)D.[2e3,1e2]
题目详情
已知方程|lnx|=kx+1在(0,e3)上有三个不等实根,则实数k的取值范围是( )
A. (0,
)2 e3
B. (
,3 e3
)2 e2
C. (
,2 e3
)1 e2
D. [
,2 e3
]1 e2
▼优质解答
答案和解析
令f(x)=kx+1,g(x)=lnx,∵y=kx+1与y=|lnx|的图象在(0,1)一定有一个交点,
依题意只需f(x)=kx+1,g(x)=lnx在(1,e3)上有2个交点即可.
作f(x)=kx+1与g(x)=lnx的图象如下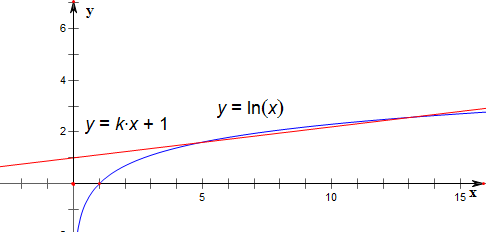
设直线f(x)=kx+1与g(x)=lnx相切于点(a,b);则
⇒k=e-2
且对数函数g(x)=lnx的增长速度越来越慢,直线f(x)=kx+1过定点(0,1)
方程|lnx|=kx+1中取x=e3得k=2e-3,∴则实数k的取值范围是
2e-3<k<e-2.
故选:C
依题意只需f(x)=kx+1,g(x)=lnx在(1,e3)上有2个交点即可.
作f(x)=kx+1与g(x)=lnx的图象如下
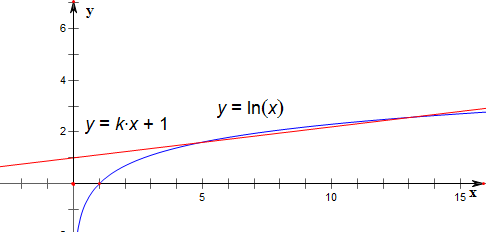
设直线f(x)=kx+1与g(x)=lnx相切于点(a,b);则
|
且对数函数g(x)=lnx的增长速度越来越慢,直线f(x)=kx+1过定点(0,1)
方程|lnx|=kx+1中取x=e3得k=2e-3,∴则实数k的取值范围是
2e-3<k<e-2.
故选:C
看了已知方程|lnx|=kx+1在...的网友还看了以下:
填方施工结束后应检查( )。 A.排水措施 B.标高 C.边坡坡度 D.压实程度 E.密实度 2020-05-18 …
测试与排错是相互联系而又性质不同的两类活动,其中排错所应具有的特征是A.证实程序有错,修改程序 2020-05-23 …
测试与排错是相互联系而性质不同的两类活动,下列哪些是排错所应具有的特征?Ⅰ.证实程序有错误Ⅱ.修 2020-05-23 …
测试与排错是相互联系而性质不同的两类活动,下列Ⅰ.证实程序有错Ⅱ.修改程序错误Ⅲ.忽视对象细节Ⅳ. 2020-05-24 …
集成测试又称整体测试,它是软件测试的重要环节,下列选项中()是对集成测试正确的描述。A.证实程序 2020-05-24 …
非粘性土料的压实程度一般用相对密度表示。() 2020-05-27 …
经过基本酸酵制作的硬质面包面团,进行烘烤得到的制品其()与面坯最后酸酵的时间有密切关系.A松软程度 2020-07-03 …
粉末状物质压实后密度测定方法,我们的具体情况是:用碾压机对飞灰样品进行多次碾压以期望增大飞灰的压实 2020-07-05 …
阅读下面文字,完成下题。虚拟疗法在“虚拟伊拉克”中的体验真实得出奇,那些战争场景被输入特制的头盔、 2020-08-01 …
世界上最结实的绳子,名字,品牌,购买地点.高分,看详细世界上最结实的绳子,名字,品牌,购买地点.(最 2020-12-07 …