早教吧作业答案频道 -->数学-->
已知函数f(x)=xlnx与直线y=m交于A(x1,y1),B(x2,y2)两点.(1)求m的取值范围;(2)求证:0<x1x2<1e2.
题目详情
已知函数f(x)=xlnx与直线y=m交于A(x1,y1),B(x2,y2)两点.
(1)求m的取值范围;
(2)求证:0<x1x2<
.
(1)求m的取值范围;
(2)求证:0<x1x2<
| 1 |
| e2 |
▼优质解答
答案和解析
(1)f(x)的定义域是(0,+∞),
f′(x)=lnx+1,
令f′(x)>0,解得:x>
,
令f′(x)<0,解得:x<
,
∴f(x)在(0,
)递减,在(
,+∞)递增,
∴f(x)min=f(
)=-
,f(1)=0,
x∈(0,
)时,f(x)<0,
画出函数图象,如图示: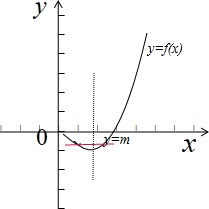
∴-
<m<0;
(2)∵x1lnx1=x2lnx2,设x1<x2,
则0<x1<
,x2>
,
要证明x1x2<
,只需证明lnx1+lnx2<-2,
令H(x)=lnx1+lnx2=lnx1+
lnx1=(1+
)lnx1,
∵x2>
,∴
<ex1,
∴H(x)<(1+ex1)lnx1,
令g(x)=(1+ex)lnx,(0<x<
),
则g′(x)=elnx+e+
,g″(x)=
,
∵x<
,∴ex-1<0,
∴g″(x)<0,g′(x)是减函数,
又g′(
)=e,∴g′(x)>g′(
),g′(x)>0,
∴g(x)是增函数,又g(
)=-2,
∴g(x)<g(
)=-2,
∴H(x)<-2,
∴0<x1x2<
.
f′(x)=lnx+1,
令f′(x)>0,解得:x>
| 1 |
| e |
令f′(x)<0,解得:x<
| 1 |
| e |
∴f(x)在(0,
| 1 |
| e |
| 1 |
| e |
∴f(x)min=f(
| 1 |
| e |
| 1 |
| e |
x∈(0,
| 1 |
| e |
画出函数图象,如图示:

∴-
| 1 |
| e |
(2)∵x1lnx1=x2lnx2,设x1<x2,
则0<x1<
| 1 |
| e |
| 1 |
| e |
要证明x1x2<
| 1 |
| e2 |
令H(x)=lnx1+lnx2=lnx1+
| x1 |
| x2 |
| x1 |
| x2 |
∵x2>
| 1 |
| e |
| x1 |
| x2 |
∴H(x)<(1+ex1)lnx1,
令g(x)=(1+ex)lnx,(0<x<
| 1 |
| e |
则g′(x)=elnx+e+
| 1 |
| x |
| ex-1 |
| x2 |
∵x<
| 1 |
| e |
∴g″(x)<0,g′(x)是减函数,
又g′(
| 1 |
| e |
| 1 |
| e |
∴g(x)是增函数,又g(
| 1 |
| e |
∴g(x)<g(
| 1 |
| e |
∴H(x)<-2,
∴0<x1x2<
| 1 |
| e2 |
看了已知函数f(x)=xlnx与直...的网友还看了以下:
求f(x)=xlnx(a-1)x1/2×2/3×3/4×4/5×…×98/99×99/1000(B 2020-05-13 …
3a的2次方b的2n+1次方与-2a的1+m次方b的2次方c的次数相同,问:x=m-2n是否为方程 2020-05-16 …
亲爱的网友:u=u2(x)u2(y)u2(z)2y-x=4mx2-(1-m)x1>0f(-x5)= 2020-06-06 …
请问:y=log0.5(2x2-3x1)x2y=24请问:y=log0.5(2x2-3x1)x2y 2020-07-19 …
说说y=log0.5(2x2-3x1)x2y=24说说y=log0.5(2x2-3x1)x2y=2 2020-07-19 …
亲爱的网友:f(x)=(根号下x^2-3x-4)/x12y-x=42X-Y3=0,L2:4X-2Y 2020-07-19 …
matlabfe(1:m,1:n)=I,这里的1:m,1:这里fe为矩阵 2020-07-24 …
亲爱的网友:f(x)=ax2bxc(a≠0)1/2×2/3×3/4×4/5×…×98/99×99/1 2020-10-31 …
亲爱的网友:f(x)=(根号下x^2-3x-4)/x11/2×2/3×3/4×4/5×…×98/99 2020-10-31 …
跪求y=lg[X√(x21)]若[x√(x21)][y(√y21)]=1limx*sin(1/x)m 2020-10-31 …