早教吧作业答案频道 -->数学-->
已知抛物线y2=8x,点Q是圆C:x2+y2+2x-8y+13=0上任意一点,记抛物线上任意一点到直线x=-2的距离为d,则|PQ|+d的最小值为()A.5B.4C.3D.2
题目详情
已知抛物线y2=8x,点Q是圆C:x2+y2+2x-8y+13=0上任意一点,记抛物线上任意一点到直线x=-2的距离为d,则|PQ|+d的最小值为( )
A. 5
B. 4
C. 3
D. 2
▼优质解答
答案和解析
如图所示,由题意知抛物线y2=8x的焦点为F(2,0),连接PF,则d=|PF|.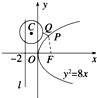
圆C的方程配方,得(x+1)2+(y-4)2=4,圆心为C(-1,4),半径r=2.
d+|PQ|=|PF|+|PQ|,
显然,|PF|+|PQ|≥|FQ|(当且仅当F,P,Q三点共线时取等号).
而|FQ|为圆C上的动点Q到定点F的距离,
显然当F,Q,C三点共线时取得最小值,
最小值为|CF|-r=
-2=5-2=3.
故选:C.

圆C的方程配方,得(x+1)2+(y-4)2=4,圆心为C(-1,4),半径r=2.
d+|PQ|=|PF|+|PQ|,
显然,|PF|+|PQ|≥|FQ|(当且仅当F,P,Q三点共线时取等号).
而|FQ|为圆C上的动点Q到定点F的距离,
显然当F,Q,C三点共线时取得最小值,
最小值为|CF|-r=
| (-1-2)2+(4-0)2 |
故选:C.
看了已知抛物线y2=8x,点Q是圆...的网友还看了以下:
验证椭圆x²/4c²+y²/3c²=1(c:半焦距)焦点到椭圆上一点最短距离为a-c=c.设该点为 2020-05-15 …
二次函数Y=ax2+bx+c,b的平方=ac,且x=0时y=-4选择则A y最大=-4B y最小= 2020-05-16 …
抛物线的顶点在原点,焦点在y轴上,抛物线上一点P(m,-3)到焦点的距离为5,则抛物线的准线方程是 2020-06-03 …
某商店售货时,其数量x与售价y关系如表所示:数量x(kg)售价y(元)18+0.4216+0.43 2020-07-30 …
定点到抛物线距离求点(4,0)到抛物线y=4/5x的最小距离,并求此时抛物线上的点的坐标 2020-07-30 …
抛物线y2=8x的准线方程是()A.x=-2B.x=-4C.y=-2D.y=-4 2020-07-31 …
已知变量x,y成负相关,且由观测数据算得样本平均数.x=3,.y=3.5,则由该观测数据算得的线性 2020-08-03 …
1,一物体做平抛运动,抛出1s后物体着地,着地时物体速度方向与水平方向成45度角,求:1,物体抛出时 2020-12-05 …
如图所示,质量为m的小球从A点水平抛出,抛出点距离地面高度为L,不计与空气的摩擦阻力,重力加速度为g 2020-12-22 …
一个物体做平抛运动,落地时的速度为50m/是,方向与水平地面成37°角,求抛出的初速度,从抛出到落地 2021-01-14 …