早教吧作业答案频道 -->数学-->
为了做好“双11”促销活动,某电商打算将进行促销活动的礼品重新包装,设计方案如下:将一块边长为20cm的正方形纸片ABCD剪去四个全等的等腰三角形△SEE′,△SFF′,△SGG′,△SHH′,再
题目详情
为了做好“双11”促销活动,某电商打算将进行促销活动的礼品重新包装,设计方案如下:将一块边长为20cm的正方形纸片ABCD剪去四个全等的等腰三角形△SEE′,△SFF′,△SGG′,△SHH′,再将剩下的阴影部分折成一个四棱锥形状的礼品袋S-EFGH,其中A,B,C,D重合于点O,E与E′重合,F与F′重合,G与G′重合,H与H′重合(如图所示),设AE=BE′=x(cm).
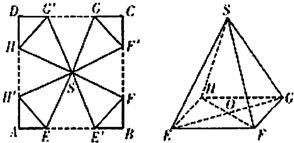
(1)求证:平面SEG⊥平面SFH;
(2)若电商要求礼品袋的侧面积不少于128cm2,试求x的取值范围;
(3)当x=5时,该电商打算将礼品袋S-EFGH全部放入一个球形状的包装盒内密封,求包装盒的内径R的最小值.

(1)求证:平面SEG⊥平面SFH;
(2)若电商要求礼品袋的侧面积不少于128cm2,试求x的取值范围;
(3)当x=5时,该电商打算将礼品袋S-EFGH全部放入一个球形状的包装盒内密封,求包装盒的内径R的最小值.
▼优质解答
答案和解析
证明:∵折后A,B,C,D重合于一点O,
∴拼接成底面EFGH的四个直角三角形必为全等的等腰直角三角形,
∴底面EFGH是正方形,故EG⊥FH,
∵在原平面EFGH是正方形,故EG⊥FH,
∵在原平面图形中,等腰三角形△SEE′≌△SGG′,
∴SE=SG,∴EG⊥SO,
又∵SO、FH⊂平面SFH,SO∩FH=O,
∴EG⊥平面SFH,
又∵EG⊂平面SEC,∴平面SEG⊥平面SFH.
(2)∵AE=BE′=x(cm).
∴EE'=20-2x,有EE'>0得0则△SEE'的高为20,
则礼品袋的侧面积S=20×20-4(S△EAH'+S△SEE')
=400-4[(
x2+
(20-2x)×10]=400-(2x2+400-40x)=-2x2+40x,
由S=-2x2+40x≥128得x2-20x+64≤0,得4≤x≤16,
∵0<x<10,∴4≤x<10.
(3)当x=5时,OE=OF=AE=5,则EF=5
,包装盒的内径最小值,
即为正四棱锥S-EFGH的外接球的半径R,
设正四棱锥的外接球的球心为O',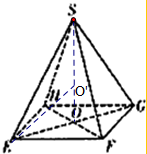
则O'在正四棱锥S-EFGH的高SO上,连接EO',
则Rt△SEO中,SO=10,
∴O'E=R,O'O=10-R,
Rt△EOO'中,OE2+O'O2=O'E2,
∴52+(10-R)2=R2,
即25+100-20R=0,得R=
=
=6.25,
即包装盒的内径R的最小值是6.25.
∴拼接成底面EFGH的四个直角三角形必为全等的等腰直角三角形,
∴底面EFGH是正方形,故EG⊥FH,
∵在原平面EFGH是正方形,故EG⊥FH,
∵在原平面图形中,等腰三角形△SEE′≌△SGG′,
∴SE=SG,∴EG⊥SO,
又∵SO、FH⊂平面SFH,SO∩FH=O,
∴EG⊥平面SFH,
又∵EG⊂平面SEC,∴平面SEG⊥平面SFH.
(2)∵AE=BE′=x(cm).
∴EE'=20-2x,有EE'>0得0
则礼品袋的侧面积S=20×20-4(S△EAH'+S△SEE')
=400-4[(
| 1 |
| 2 |
| 1 |
| 2 |
由S=-2x2+40x≥128得x2-20x+64≤0,得4≤x≤16,
∵0<x<10,∴4≤x<10.
(3)当x=5时,OE=OF=AE=5,则EF=5
| 2 |
即为正四棱锥S-EFGH的外接球的半径R,
设正四棱锥的外接球的球心为O',

则O'在正四棱锥S-EFGH的高SO上,连接EO',
则Rt△SEO中,SO=10,
∴O'E=R,O'O=10-R,
Rt△EOO'中,OE2+O'O2=O'E2,
∴52+(10-R)2=R2,
即25+100-20R=0,得R=
| 125 |
| 20 |
| 25 |
| 4 |
即包装盒的内径R的最小值是6.25.
看了为了做好“双11”促销活动,某...的网友还看了以下:
电子商务判断题(最好边上能注解)1.电子商务的本质是商务.()2.电子商务就是指电子交易.()3. 2020-05-17 …
电子商务按照运作方式分为(19)。A.完全电子商务和非完全电子商务B.B2B电子商务和B2C电子商务 2020-05-26 …
下列应用哪些属于网络应用(多选)A.email电子邮件B.Web浏览C.即时通讯D.电子商务E.FT 2020-05-26 …
问一下《基本乐理教程》练习七第四题和第九题的答案写出下列调式的调号并写上宫音与主音:F商G羽A角D 2020-06-11 …
英语翻译移动电子商务(MobileE-Commerce)是由电子商务(E-Commerce)的定义 2020-07-04 …
下列工具:A、钢丝钳B、镊子C、剪铁剪刀D、理发剪刀E、羊角锤F、筷子G、扫把H、扳手I、开汽水起 2020-07-07 …
“北京HTD电子商务有限责任有限公司”翻印成英文后是什么?重点是“电子商务”这个词的翻译,Beij 2020-07-23 …
电子商务名词解释!是电子商务课的!:1网络2内/外联网3电子支票4现代物流技术5数字支票解答题:1什 2020-11-07 …
随着信息技术的发展,电子商务(E-business)、电子银行(E-banking)、电子政务(E- 2020-11-27 …
(2010•宝坻区一模)生活中掌握一些安全用电的常识很有必要,以下做法中正确的是()A.保险丝可以用 2021-01-07 …