如图，在边长为7的正方形ABCD中，点M是对角线BD上的一点，过点M作ME∥CD交BC于点E，作MF∥BC交CD于点F．请解答下列问题：（1）试探究线段AM与EF的大小关系并说明理由；（2）若BE=4，求

Question

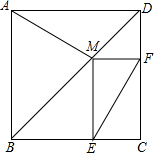如图，在边长为7的正方形ABCD中，点M是对角线BD上的一点，过点M作ME∥CD交BC于点E，作MF∥BC交CD于点F．请解答下列问题：
（1）试探究线段AM与EF的大小关系并说明理由；
（2）若BE=4，求AM的长．

Answer 1

考点：
正方形的性质 全等三角形的判定与性质
专题：

分析：
（1）可先证明四边形APMQ是矩形，再证明△ABM≌△CBM，可证得AM=CM=EF；（2）先求得EC，由勾股定理可求得EF，由（1）可得AM的长．

（1）AM=EF，理由：∵ME∥CD，MF∥BC，∠C=90°，∴四边形CEMF是矩形，∴CM=EF，连接MC，在△ABM和△CBM中，AB=BC∠ABM=∠CBMBM=BM，∴△ABM≌△CBM（SAS），∴AM=CM=EF；（2）∵BC=7，BE=4，∴EC=3，在Rt△EFC中，可求得EF=5，∴AM=EF=5．
点评：
本题主要考查正方形的性质及矩形的判定，先判定出四边形CEMF是矩形得到CM=EF是解题的关键．