早教吧作业答案频道 -->数学-->
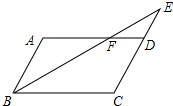
如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=12CD.(1)求证:△ABF∽△CEB;(2)若△DEF的面积为2,求平行四边形ABCD的面积.
题目详情
如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=
CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求平行四边形ABCD的面积.
| 1 |
| 2 |

(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求平行四边形ABCD的面积.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,
∴∠ABF=∠CEB,
∴△ABF∽△CEB;
 (2) ∵四边形ABCD是平行四边形,
(2) ∵四边形ABCD是平行四边形,
∴AD∥BC,AB平行且等于CD,
∴△DEF∽△CEB,△DEF∽△ABF,
∵DE=
CD,
∴
=(
)2=
,
=(
)2=
,
∵S△DEF=2,
∴S△CEB=18,S△ABF=8,
∴S四边形BCDF=S△BCE-S△DEF=16,
∴S四边形ABCD=S四边形BCDF+S△ABF=16+8=24.
∴∠A=∠C,AB∥CD,
∴∠ABF=∠CEB,
∴△ABF∽△CEB;
 (2) ∵四边形ABCD是平行四边形,
(2) ∵四边形ABCD是平行四边形,∴AD∥BC,AB平行且等于CD,
∴△DEF∽△CEB,△DEF∽△ABF,
∵DE=
| 1 |
| 2 |
∴
| S△DEF |
| S△CEB |
| DE |
| CE |
| 1 |
| 9 |
| S△DEF |
| S△ABF |
| DE |
| AB |
| 1 |
| 4 |
∵S△DEF=2,
∴S△CEB=18,S△ABF=8,
∴S四边形BCDF=S△BCE-S△DEF=16,
∴S四边形ABCD=S四边形BCDF+S△ABF=16+8=24.
看了 如图,平行四边形ABCD中,...的网友还看了以下:
1、核酸从头中,嘌呤环的第一位氮来自()A、天冬氨酸B、氨甲酰磷酸C、甘氨酸D、谷氨酰酸2、别构酶 2020-06-05 …
中学的平面几何求证问题,在直角三角形中,角C为90度,AC=BC,AD是角A的平分线,从B做AD的 2020-06-06 …
已知梯形ABCD,AD平行BC,对角线AC,BD相交於点O,A',B',C',D'分别是AO,BO 2020-06-07 …
图①,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点E,直线BM、CN 2020-06-12 …
三角形ABC,AD垂直于BC,并且AD为角A平分线,请问能否用三线合一来证,若不能请写你的证法三角 2020-07-15 …
已知BE和CF是三角形ABC两边上的高,BE=CF,H是BE和CF的交点,求证HB=HC2题已知四 2020-07-15 …
1.四边形ABCD和四边形A'B'C'D'中,AB:A'B'=BC:B'C'=CB:C'D'=DA 2020-07-25 …
点A(X1,Y1),B(X2,Y2)是抛物线C:X^2=2Y上的不同两点,过A,B分别作抛物线C的 2020-07-30 …
已知双曲线C的渐近线方程为y=±x,一个焦点为(22,0).(1)求双曲线C的方程;(2)过双曲线 2020-07-31 …
证明相似三角形的高三角形ABC相似三角形A'B'C'相似比为K,AD,A'D'分别是三角形ABC和 2020-08-01 …