四边形ABCD内接于圆，另一圆的圆心在边AB上且与其余三边相切，求证：AD+BC=AB．

Question

四边形ABCD内接于圆，另一圆的圆心在边AB上且与其余三边相切，求证：AD+BC=AB．

Answer 1

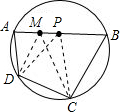证明：设AB上的圆心为P，在AB上取一点M，使MB=BC，
连接MC，MD，PD，PC 等腰△CMB中，∠CMB=∠MCB，
∴∠CMB=(1)/(2)（∠MCB+∠CMB），
=(1)/(2)（180°-∠B），
=(1)/(2)∠ADC （圆内接四边形ABCD的对角相加为180°），
=∠PDC （设圆P切AD于E，切DC于F，有PE=PF，Rt△PDE和Rt△PDF中，一对儿直角边相等，且斜边是公共的，∴两Rt△全等，可得PD平分∠CDA），
∴M，P，C，D四点共圆，
∴∠AMD=∠DCP，
=(1)/(2)∠DCB （同理，可证PC平分∠DCB），
=(1)/(2)（180°-∠A） （ABCD的另一对儿对角和为180°，
=(1)/(2)（∠ADM+∠AMD），
∴∠AMD=∠ADM，
∴AD=AM，
∴AD+BC=AM+MB=AB．