早教吧作业答案频道 -->数学-->
等边三角形ABC的边长为23,在AC,BC边上各有一个动点E,F,满足AE=CF,连接AF,BE相交于点P.(1)∠APB的度数;(2)当E从点A运动到点C时,试求点P经过的路径长;(3)连结CP,直接写出CP长
题目详情
等边三角形ABC的边长为2
,在AC,BC边上各有一个动点E,F,满足AE=CF,连接AF,BE相交于点P.
(1)∠APB的度数;
(2)当E从点A运动到点C时,试求点P经过的路径长;
(3)连结CP,直接写出CP长度的最小值.
| 3 |
(1)∠APB的度数;
(2)当E从点A运动到点C时,试求点P经过的路径长;
(3)连结CP,直接写出CP长度的最小值.
▼优质解答
答案和解析
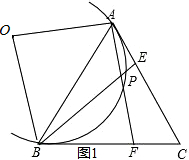 (1)∵△ABC为等边三角形,
(1)∵△ABC为等边三角形,
∴AB=AC,∠C=∠CAB=60°,
又∵AE=CF,
在△ABE和△CAF中,
,
∴△ABE≌△CAF(SAS),
∴AF=BE,∠ABE=∠CAF.
又∵∠APE=∠BPF=∠ABP+∠BAP,
∴∠APE=∠BAP+∠CAF=60°.
∴∠APB=180°-∠APE=120°.
(2)如图1,∵AE=CF,
∴点P的路径是一段弧,由题目不难看出当E为AC的中点的时候,点P经过弧AB的中点,此时△ABP为等腰三角形,且∠ABP=∠BAP=30°,
∴∠AOB=120°,
又∵AB=2
,
∴OA=2,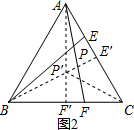
点P的路径是l=
=
=
;
(3)如图2,∵AE=CF,
∴点P的路径是一段弧,
∴当点E运动到AC的中点时,CP长度的最小,
即点P为△ABC的中心,
过B作BE′⊥AC于E′,
∴PC=
BE′,
∵△ABC是等边三角形,
∴BE′=
BC=3,
∴PC=2.
∴CP长度的最小值是2.
 (1)∵△ABC为等边三角形,
(1)∵△ABC为等边三角形,∴AB=AC,∠C=∠CAB=60°,
又∵AE=CF,
在△ABE和△CAF中,
|
∴△ABE≌△CAF(SAS),
∴AF=BE,∠ABE=∠CAF.
又∵∠APE=∠BPF=∠ABP+∠BAP,
∴∠APE=∠BAP+∠CAF=60°.
∴∠APB=180°-∠APE=120°.
(2)如图1,∵AE=CF,
∴点P的路径是一段弧,由题目不难看出当E为AC的中点的时候,点P经过弧AB的中点,此时△ABP为等腰三角形,且∠ABP=∠BAP=30°,
∴∠AOB=120°,
又∵AB=2
| 3 |
∴OA=2,

点P的路径是l=
| nπr |
| 180 |
| 120•π×2 |
| 180 |
| 4π |
| 3 |
(3)如图2,∵AE=CF,
∴点P的路径是一段弧,
∴当点E运动到AC的中点时,CP长度的最小,
即点P为△ABC的中心,
过B作BE′⊥AC于E′,
∴PC=
| 2 |
| 3 |
∵△ABC是等边三角形,
∴BE′=
| ||
| 2 |
∴PC=2.
∴CP长度的最小值是2.
看了 等边三角形ABC的边长为23...的网友还看了以下:
如图,已知角3=角1+角2,求证角A+角B+角C+角D=180°俺脑子反应慢,希望回答问题的朋友可 2020-04-05 …
如图,在四边形abcd中,(1)ac平分角bad,角1=角d,求证:cb=cd.(2)若cb=cd 2020-04-11 …
c是线段ab上的一点,ad//BE,角d=角1,角1=角2,求角dce的度数. 2020-04-27 …
已知,如图,角2+角D=180度,角1=角B,求证:AB//EF,中间的是图 2020-05-14 …
已知,角2+角d=180度,角1=角b.求证:ab//ef 2020-05-14 …
如图,角2+角d=180度,角1=角b,求证ab平行ef 2020-05-14 …
如图,已知AB垂直于MN与B,CD垂直于MN与D,角3=3倍的角1-角2,求角1,角2的度数. 2020-05-16 …
如图DB垂直于AC,DC垂直于AD,且角1=角2,求AB垂直于BC大哥大姐求求想想啊- - 2020-06-27 …
已知:如图,BP交CD于P,角ABP+角BPC=180度,角1=角2,求证EB平行于PF不要图. 2020-07-24 …
已知角1,角2,求做作一个角,使它等于2倍角1减角2. 2020-11-06 …