早教吧作业答案频道 -->数学-->
如图,已知点A是线段OB的垂直平分线上一点,AN⊥ON,BO⊥ON,P为ON上一点,∠OPB=∠OAB.(1)若∠AOB=60°,PB=4,则OP=;(2)在(1)的条件下,求证:PA+PO=PB;(3)如图②,若ON=5,求出PO
题目详情
如图,已知点A是线段OB的垂直平分线上一点,AN⊥ON,BO⊥ON,P为ON上一点,∠OPB=∠OAB.
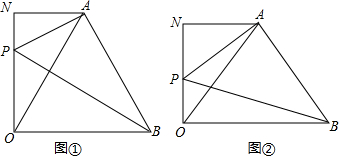
(1)若∠AOB=60°,PB=4,则OP=___;
(2)在(1)的条件下,求证:PA+PO=PB;
(3)如图②,若ON=5,求出PO+PB的值.

(1)若∠AOB=60°,PB=4,则OP=___;
(2)在(1)的条件下,求证:PA+PO=PB;
(3)如图②,若ON=5,求出PO+PB的值.
▼优质解答
答案和解析
(1)∵点A是线段OB的垂直平分线上一点,
∴AO=AB.
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB,∠OAB=∠ABO=60°.
∴∠OPB=∠OAB=60°.
∵BO⊥ON,即∠POB=90°,
∴∠OBP=30°,
∴OP=
PB=
×4=2.
故答案为2;
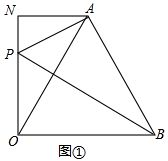
(2)证明:如图①,
由(1)得OB=AB,∠OAB=∠ABO=60°,∠OBP=30°,
∴∠ABP=∠ABO-∠OBP=30°=∠OBP.
在△OBP和△ABP中,
,
∴△OBP≌△ABP(SAS),
∴OP=AP=2,
∴PA+PO=4=PB;
(3)延长ON、BA交于点D,如图②.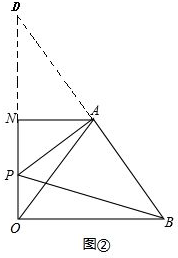
∵AO=AB,∴∠AOB=∠ABO.
∵∠DOB=90°,
∴∠D+∠OBD=90°,∠AOD+∠BOA=90°,
∴∠D=∠AOD,
∴AD=AO.
∵AN⊥OD,
∴DN=ON=5.
∵∠OPB=∠OAB,
∴∠AOD=∠PBD,
∴∠D=∠PBD,
∴PD=PB,
∴PO+PB=PO+PD=OD=10.
∴AO=AB.
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB,∠OAB=∠ABO=60°.
∴∠OPB=∠OAB=60°.
∵BO⊥ON,即∠POB=90°,
∴∠OBP=30°,
∴OP=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为2;

(2)证明:如图①,
由(1)得OB=AB,∠OAB=∠ABO=60°,∠OBP=30°,
∴∠ABP=∠ABO-∠OBP=30°=∠OBP.
在△OBP和△ABP中,
|
∴△OBP≌△ABP(SAS),
∴OP=AP=2,
∴PA+PO=4=PB;
(3)延长ON、BA交于点D,如图②.

∵AO=AB,∴∠AOB=∠ABO.
∵∠DOB=90°,
∴∠D+∠OBD=90°,∠AOD+∠BOA=90°,
∴∠D=∠AOD,
∴AD=AO.
∵AN⊥OD,
∴DN=ON=5.
∵∠OPB=∠OAB,
∴∠AOD=∠PBD,
∴∠D=∠PBD,
∴PD=PB,
∴PO+PB=PO+PD=OD=10.
看了 如图,已知点A是线段OB的垂...的网友还看了以下:
对n个记录的文件进行归并排序,所需要的辅助存储空间为 A.O(1) B.O(n) C.O(log2n 2020-05-23 …
对包含n个元素的散列表进行检索,平均检索长度为( )。A.O(log2n)B.O(n)C.O(n*l 2020-05-23 …
对n个记录的文件进行堆排序,最坏情况下的执行时间为A.O(log2n)B.O(n)C.O(n log 2020-05-23 …
对n个元素进行堆排序时,其空间复杂度为()。A.O(log2n)B.O(n log2n)C.O(n) 2020-05-24 …
A.O(1),O(1)B.O(n),O(1)C.O(n2),O(1)D.O(n),O(n) 2020-05-26 …
A.O(n2)B.O(n)C.O(n-1)D.O(n+1) 2020-05-26 …
如果所有关键字都相等,那么插入排序算法的时间复杂度为A.O(1)B.O(n)C.O(nlogn)D 2020-07-23 …
算法时间复杂度问题,谢谢!最好有解释假设算法A1和算法A2都可以解决规模为n的问题P,且时间复杂度都 2020-10-31 …
关于渐进时间复杂度题已知某一算法的时间复杂度上限函数满足递归关系T(n)=2(T/2)+n,那么该算 2021-01-14 …
3.下面算法的时间复杂度为?3.下面算法的时间复杂度为。intf(unsignedintn){if( 2021-01-14 …