早教吧作业答案频道 -->数学-->
如图,在几何体ABCDEF中,等腰梯形ABCD所在的平面与正方形CDEF所在的平面互相垂直,已知AB∥CD,AB=2BC=4,∠ABC=60°,点M是线段AC的中点.(Ⅰ)求证:CF⊥AD;(Ⅱ)求证:ME∥平面BCF;(Ⅲ
题目详情
如图,在几何体ABCDEF中,等腰梯形ABCD所在的平面与正方形CDEF所在的平面互相垂直,已知AB∥CD,AB=2BC=4,∠ABC=60°,点M是线段AC的中点.
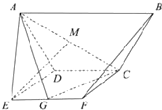
(Ⅰ)求证:CF⊥AD;
(Ⅱ)求证:ME∥平面BCF;
(Ⅲ)对于线段EF上的任意一点G,是否总有平面ACG⊥平面BCF,并说明理由.

(Ⅰ)求证:CF⊥AD;
(Ⅱ)求证:ME∥平面BCF;
(Ⅲ)对于线段EF上的任意一点G,是否总有平面ACG⊥平面BCF,并说明理由.
▼优质解答
答案和解析
证明:(Ⅰ)由正方形CDEF,得CF⊥CD,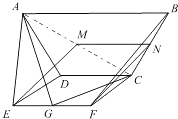
∵平面ABCD⊥平面CDEF,且平面ABCD∩平面CDEF=CD,
∴CF⊥平面ABCD,
又∵AD⊂平面ABCD,∴CF⊥AD.
(Ⅱ)如图,取BC中点N,连结MN、NF,
则MN∥AB,且MN=
AB=2,
又∵EF∥CD,CD∥AB,∴EF∥MN,
∵AB=2BC=4,∠ABC=60°,
∴CD=2,∴EF=MN,
∴四边形EFNM是平行四边形,∴ME∥FN,
又∵ME⊄平面EFNM,FN⊂平面BCF,
∴ME∥平面BCF.
(Ⅲ)对于线段EF上的任意一点G,总有平面ACG⊥平面BCF.
理由如下:
∵AB=2BC=4,∠ABC=60°,
在△ABC中,由余弦定理得:
AC2=AB2+BC2-2AB•BC•cos60°=16+4-2×4×2×cos60°=12,
∴AC=2
,∴AB2=AC2+BC2,∴AC⊥BC,
由(Ⅰ)知CF⊥平面ABCD,
∵AC⊂平面ABCD,∴CF⊥AC,
∵CF∩BC=C,且CF,BC⊂平面BCF,
∴AC⊥平面BCF,
又∵AC⊂平面ACG,∴平面ACG⊥平面BCF,
∴对于线段EF上的任意一点G,总有平面ACG⊥平面BCF.

∵平面ABCD⊥平面CDEF,且平面ABCD∩平面CDEF=CD,
∴CF⊥平面ABCD,
又∵AD⊂平面ABCD,∴CF⊥AD.
(Ⅱ)如图,取BC中点N,连结MN、NF,
则MN∥AB,且MN=
| 1 |
| 2 |
又∵EF∥CD,CD∥AB,∴EF∥MN,
∵AB=2BC=4,∠ABC=60°,
∴CD=2,∴EF=MN,
∴四边形EFNM是平行四边形,∴ME∥FN,
又∵ME⊄平面EFNM,FN⊂平面BCF,
∴ME∥平面BCF.
(Ⅲ)对于线段EF上的任意一点G,总有平面ACG⊥平面BCF.
理由如下:
∵AB=2BC=4,∠ABC=60°,
在△ABC中,由余弦定理得:
AC2=AB2+BC2-2AB•BC•cos60°=16+4-2×4×2×cos60°=12,
∴AC=2
| 3 |
由(Ⅰ)知CF⊥平面ABCD,
∵AC⊂平面ABCD,∴CF⊥AC,
∵CF∩BC=C,且CF,BC⊂平面BCF,
∴AC⊥平面BCF,
又∵AC⊂平面ACG,∴平面ACG⊥平面BCF,
∴对于线段EF上的任意一点G,总有平面ACG⊥平面BCF.
看了 如图,在几何体ABCDEF中...的网友还看了以下:
由实数a,-a,a的绝对值,2次根号下a的平方,3次根号下a的立方所组成的集合所含的元素个数最多的 2020-04-05 …
下列项目中,关于金融资产转移会计处理的说法错误的是???A.出售金融资产时,因不附追索权,与该金融 2020-06-17 …
中方动用了5名队员,就击败了日方所有队员.这样的过程有几种?中日围棋队各出了7名队员,按安排好的次 2020-06-28 …
关于魔方,不会公式但是会玩我不会3阶魔方的公式,所以我的速度只能在50秒到1分多钟,我想更快复原魔 2020-07-04 …
成语中的牛字有哪几方面的寓意?即牛字所包含的寓意是什么?有哪几方面?最好附上一些解释牛字的某层寓意 2020-07-24 …
X^3=8是否为一元三次?如果将它整理,两边同时开三次根号,就得:X=2老师说看一个方程要整理成最 2020-08-02 …
高一地理必须知道的几个地方的时区高中地理需要知道哪几个地方所在的时区?比如北京在东八区这样,需要记住 2020-11-21 …
把915连续写几次,所组成的数就能被9整除,并且这个数最小.把915连续写几次,所组成的数就能被9整 2020-11-28 …
有一天,上帝把所有的有一天,上帝把所有的动物们都找去,问它们对自己有没有什么不满意的地方.一问方知, 2020-12-06 …
一天,上帝把所有的动物都找去,问他们对自己有什么不满意的地方。一问方知,几乎所有的动物都对自己不满意 2020-12-06 …