早教吧作业答案频道 -->数学-->
如图,已知正方体ABCD-A1B1C1D1的棱长为6,点E、F分别是BB1、DD1的中点.(1)求证:平面AEC1F⊥平面ACC1A1;(2)求多面体AEC1FA1B1的体积.
题目详情
如图,已知正方体ABCD-A1B1C1D1的棱长为6,点E、F分别是BB1、DD1的中点.
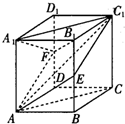
(1)求证:平面AEC1F⊥平面ACC1A1;
(2)求多面体AEC1FA1B1的体积.

(1)求证:平面AEC1F⊥平面ACC1A1;
(2)求多面体AEC1FA1B1的体积.
▼优质解答
答案和解析
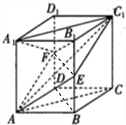 (1)证明:连接EF,BD,则
(1)证明:连接EF,BD,则
∵点E、F分别是BB1、DD1的中点,
∴AE=EC1=C1F=FA,
∴四边形AEC1F为菱形,
∴EF⊥AC1,
∵AA1⊥平面ABCD,
∴AA1⊥BD,
∵EF∥BD,
∴EF⊥AA1,
∵EF⊥AC1,EF⊥AA1,AA1∩AC1=A,
∴EF⊥平面ACC1A1,
∵EF⊂平面AEC1F,∴平面AEC1F⊥平面ACC1A1;
(2) ∵正方体ABCD-A1B1C1D1的棱长为6,
∴VC1-AFA1=
×S△AFA1×6=36,
∵点E是BB1的中点,BB1=6,
∴B1E=3,
∴SAEB1A1=
•(3+6)•6=27
∴VC1-AEB1A1=
•
•(3+6)•6•6=54,
∴多面体AEC1FA1B1的体积=36+54=90.
 (1)证明:连接EF,BD,则
(1)证明:连接EF,BD,则∵点E、F分别是BB1、DD1的中点,
∴AE=EC1=C1F=FA,
∴四边形AEC1F为菱形,
∴EF⊥AC1,
∵AA1⊥平面ABCD,
∴AA1⊥BD,
∵EF∥BD,
∴EF⊥AA1,
∵EF⊥AC1,EF⊥AA1,AA1∩AC1=A,
∴EF⊥平面ACC1A1,
∵EF⊂平面AEC1F,∴平面AEC1F⊥平面ACC1A1;
(2) ∵正方体ABCD-A1B1C1D1的棱长为6,
∴VC1-AFA1=
| 1 |
| 3 |
∵点E是BB1的中点,BB1=6,
∴B1E=3,
∴SAEB1A1=
| 1 |
| 2 |
∴VC1-AEB1A1=
| 1 |
| 3 |
| 1 |
| 2 |
∴多面体AEC1FA1B1的体积=36+54=90.
看了 如图,已知正方体ABCD-A...的网友还看了以下:
正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,BB1上的点,则三棱锥D1-E 2020-05-16 …
点x=1是函数y={[e^(1/x-1)-1}/{[e^(1/x-1)+1]}的跳跃间断点,当x从 2020-05-16 …
求指数分布中分布密度λe^-λx积分后为1-e^-λx的具体过程,学概率论时补下微积分,不容易呀, 2020-06-10 …
正方体ABCD-A'B'C'D'的棱长为1,E,F,N分别为BD,AB1,AB上的点,且BE:BD 2020-06-21 …
正方体ABCD-A'B'C'D'的棱长为1,E,F,N分别为BD,AB1,AB上的点,且BE:BD 2020-06-21 …
棱锥一题!正方形ABCD的边长为1,E、F分别是BC、CD的中点,沿AE、EF、AF折成一个三棱锥 2020-06-21 …
非索非那定(E)可用于减轻季节性过敏鼻炎引起的症状。其合成路线如下(其中R-为)(1)E中的含氧官 2020-07-07 …
正方体ABCD-A1B1C1D1棱长为1,E,F分别为棱BC,DD1上的点,如果B1E垂直于平面AB 2020-11-03 …
1、工人师傅从一块废铁皮上剪下四个圆做冲击垫,要求每个圆的面积都是12.56cm²,那么这块铁皮的边 2020-11-20 …
正方形ABCD边长为1,E、F分别为BC、CD中点,沿AE、EF、AF折成一个三棱锥,使B、C、D三 2021-01-04 …