早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,D,E分别为AB,CD的中点,AE的延长线交CB于F.现将△ACD沿CD折起,折成二面角A-CD-B,连接AF.(I)求证:平面AEF⊥平面CBD;(II)当二面角A-CD-B为直二面
题目详情
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,D,E分别为AB,CD的中点,AE的延长线交CB于F.现将△ACD沿CD折起,折成二面角A-CD-B,连接AF.
(I)求证:平面AEF⊥平面CBD;
(II)当二面角A-CD-B为直二面角时,求直线AB与平面CBD所成角的正切值.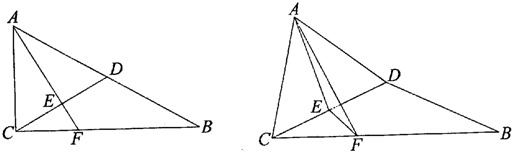
(I)求证:平面AEF⊥平面CBD;
(II)当二面角A-CD-B为直二面角时,求直线AB与平面CBD所成角的正切值.

▼优质解答
答案和解析
 (I)证明:在Rt△ABC中,D为AB的中点,
(I)证明:在Rt△ABC中,D为AB的中点,
得AD=CD=DB,又∠B=30°,得△ACD是正三角形,
又E是CD的中点,得AE⊥CD.(3分)
折起后,AE⊥CD,EF⊥CD,
又AE∩EF=E,AE⊂平面AED,EF⊂平面AEF,
故CD⊥平面AEF,(6分)
又CD⊂平面CDB,
故平面AEF⊥平面CBD.(7分)
(II) ∵二面角A-CD-B是直二面角,
且AE⊥CD,∴AE⊥平面CBD.(8分)
连接EB,AB,则∠ABE就是直线AB与
平面CBD所成的角.(9分)
设AC=a,在△CDB中,
∠DCB=30°,CE=
,CB=
a,
∴EB2=CE2+CB2-2CE•CB•cos∠DCB=
a2,又AE=
a,在Rt△AEB中,tan∠ABE=
=
=
.
∴直线AB与平面CBD所成角的正切值为
.(14分)
 (I)证明:在Rt△ABC中,D为AB的中点,
(I)证明:在Rt△ABC中,D为AB的中点,得AD=CD=DB,又∠B=30°,得△ACD是正三角形,
又E是CD的中点,得AE⊥CD.(3分)
折起后,AE⊥CD,EF⊥CD,
又AE∩EF=E,AE⊂平面AED,EF⊂平面AEF,
故CD⊥平面AEF,(6分)
又CD⊂平面CDB,
故平面AEF⊥平面CBD.(7分)
(II) ∵二面角A-CD-B是直二面角,
且AE⊥CD,∴AE⊥平面CBD.(8分)
连接EB,AB,则∠ABE就是直线AB与
平面CBD所成的角.(9分)
设AC=a,在△CDB中,
∠DCB=30°,CE=
| a |
| 2 |
| 3 |
∴EB2=CE2+CB2-2CE•CB•cos∠DCB=
| 7 |
| 4 |
| ||
| 2 |
| AE |
| EB |
| ||||
|
| ||
| 7 |
∴直线AB与平面CBD所成角的正切值为
| ||
| 7 |
看了 如图,在Rt△ABC中,∠A...的网友还看了以下:
在三棱锥A-BCD中,E在棱AB上,F在棱CD上,且AE/EB=CF/FD=入(入>0)设α为异面 2020-04-24 …
They can't have been doing thier homework.have be 2020-05-16 …
求球面:x^2+y^2+z^2=a^2含在圆柱面x^2+y^2=ax内部的那部分面积.由于对称可以 2020-05-16 …
在正四面体ABCD中,M,N分别为BC,AD的中点,求异面直线MN与BD所成的角在正四面体(四个面 2020-06-04 …
一个成语形容平常默默不问其实一直在为后面的崛起做准备! 2020-06-08 …
一滴体积为V0的油酸,配制成体积比为l:n的油酸溶液(n>1),现取一滴体积仍为V0的油酸溶液滴在 2020-06-12 …
某校为美化校园,计划对面积为1800平方米的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能 2020-06-16 …
某校为美化校园,计划对面积为2000m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成 2020-11-04 …
某校为美化校园,计划对面积为1800平方米区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成 2020-11-04 …
如图,左图为一个边长为4的正方形,右图为左图的表面展开图(字在外表面上),请根据要求回答问题:(1) 2020-11-10 …