早教吧作业答案频道 -->数学-->
如图,菱形ABCD中∠A=60°,过点C的直线分别交AB、AD的延长线于E、F,BF与DE相交于M.求证:(1)BD是BE和DF的比例中项;(2)BD是DM和DE的比例中项.
题目详情
如图,菱形ABCD中∠A=60°,过点C的直线分别交AB、AD的延长线于E、F,BF与DE相交于M.求证:
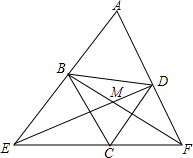
(1)BD是BE和DF的比例中项;
(2)BD是DM和DE的比例中项.

(1)BD是BE和DF的比例中项;
(2)BD是DM和DE的比例中项.
▼优质解答
答案和解析
(1)∵ 四边形ABCD是菱形,
四边形ABCD是菱形,
∴AB=AD=BC=CD,AB∥CD,AD∥BC,
∴∠EBC=∠A=∠CDF,∠AEF=∠DCF,
∴△BCE∽△CDF,
∴
=
,
∵∠A=60°,
∴△ABD是等边三角形,
∴BD=BC=CD,
∴
=
,
∴BD2=BE•DF,
即BD是BE和DF的比例中项;
(2)∵
=
,
∵∠EBD=∠BDF=120°,
∴△DBE∽△FBD,
∴∠BED=∠FBD,
∵∠BDM=∠BDE,
∴△BDM∽△EBD,
∴
=
,
∴BD2=DE•DM,
即BD是DM和DE的比例中项.
 四边形ABCD是菱形,
四边形ABCD是菱形,∴AB=AD=BC=CD,AB∥CD,AD∥BC,
∴∠EBC=∠A=∠CDF,∠AEF=∠DCF,
∴△BCE∽△CDF,
∴
| BE |
| CD |
| BC |
| DF |
∵∠A=60°,
∴△ABD是等边三角形,
∴BD=BC=CD,
∴
| BE |
| BD |
| BD |
| DF |
∴BD2=BE•DF,
即BD是BE和DF的比例中项;
(2)∵
| BE |
| BD |
| BD |
| DF |
∵∠EBD=∠BDF=120°,
∴△DBE∽△FBD,
∴∠BED=∠FBD,
∵∠BDM=∠BDE,
∴△BDM∽△EBD,
∴
| BD |
| DE |
| DM |
| BD |
∴BD2=DE•DM,
即BD是DM和DE的比例中项.
看了 如图,菱形ABCD中∠A=6...的网友还看了以下:
如图中1-6题数学选择填空题求答案 2020-05-16 …
小球从靠近竖直砖墙的某位置由静止释放,用频闪方法拍摄的小球位置如图中1、2、3和4所示.已知连续两 2020-06-15 …
(2012•台州二模)下丘脑是机体调节内分泌活动的枢纽,与体内的许多生理活动密切相关,下丘脑与垂体 2020-06-21 …
易语言怎么表达1-81数中,比如其中1、3、5、6、7、8、11.....为吉。2、4、9、10、 2020-07-14 …
将前15个正整数1,2,…,15分成五组,每组3个数.若每组中的3个数之和都相等,就称这种分组方案 2020-07-20 …
如图中∠1和∠2是同位角的是()A.(1)(2)(3)B.(1)(2)(5)C.(3)(4)(5) 2020-07-23 …
如图,点o是线段ab的中点,AB=24cm.(1)如果M,N亮点把线段AB分成1:4:3三部分,求 2020-07-25 …
如图是DNA分子的结构模式图,请据图回答:(1)用文字写出如图中1-10的名称:①②③④⑤⑥⑦⑧⑨ 2020-07-29 …
如图中1~7以及A、B、C表示人体消化系统组成的部分器官,而①~⑥是部分器官的功能,请据图回答:( 2020-07-29 …
k阶子式所对应的代数余子式中-1的幂次如何确定比如图中-1的幂次为1+2+...+r+1+2+.. 2020-08-03 …