三棱锥A­BCD及其侧视图、俯视图如图1­4所示．设M，N分别为线段AD，AB的中点，P为线段BC上的点，且MN⊥NP.(1)证明：P是线段BC的中点；(2)求二面角A­

Question

三棱锥 A ­ BCD 及其侧视图、俯视图如图1­4所示．设 M ， N 分别为线段 AD ， AB 的中点， P 为线段 BC 上的点，且 MN ⊥ NP .

(1)证明： P 是线段 BC 的中点；

(2)求二面角 A ­ NP ­ M 的余弦值．

　

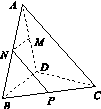
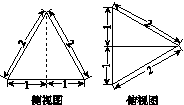
图1­4

Answer 1

(1)如图所示，取BD的中点O，连接AO，CO. 由侧视图及俯视图知，△ABD，△BCD为正三角形， 所以AO⊥BD，OC⊥BD. 因为AO，OC⊂平面AOC，且AO∩OC＝O， 所以BD⊥平面AOC. 又因为AC⊂平面AOC，所以BD⊥AC. 取BO的中点H，连接NH，PH. 又M，N，H分别为线段AD，AB，BO的中点，所以MN∥BD，NH∥AO， 因为AO⊥BD，所以NH⊥BD. 因为MN⊥NP，所以NP⊥BD. 因为NH，NP⊂平面NHP，且NH∩NP＝N，所以BD⊥平面NHP. 又因为HP⊂平面NHP，所以BD⊥HP. 又OC⊥BD，HP⊂平面BCD，OC⊂平面BCD，所以HP∥OC. 因为H为BO的中点，所以P为BC的中点． (2)方法一：如图所示，作NQ⊥AC于Q，连接MQ. 由(1)知，NP∥AC，所以NQ⊥NP. 因为MN⊥NP，所以∠MNQ为二面角A ­ NP ­ M的一个平面角． 由(1)知，△ABD，△BCD为边长为2的正三角形，所以AO＝OC＝. 由俯视图可知，AO⊥平面BCD. 因为OC⊂平面BCD，所以AO⊥OC，因此在等腰直角△AOC中，AC＝. 作BR⊥AC于R 因为在△ABC中，AB＝BC，所以R为AC的中点， 所以BR＝＝. 因为在平面ABC内，NQ⊥AC，BR⊥AC， 所以NQ∥BR. 又因为N为AB的中点，所以Q为AR的中点， 所以NQ＝＝. 同理，可得MQ＝. 故△MNQ为等腰三角形， 所以在等腰△MNQ中， cos∠MNQ＝＝＝. 故二面角A ­ NP ­ M的余弦值是. 方法二：由俯视图及(1)可知，AO⊥平面BCD. 因为OC，OB⊂平面BCD，所以AO⊥OC，AO⊥OB. 又OC⊥OB，所以直线OA，OB，OC两两垂直． 如图所示，以O为坐标原点，以OB，OC，OA的方向为x轴，y轴，z轴的正方向，建立空间直角坐标系O ­xyz. 则A(0，0，)，B(1，0，0)，C(0，，0)，D(－1，0，0)． 因为M，N分别为线段AD，AB的中点， 又由(1)知，P为线段BC的中点， 所以M，N，P，于是AB＝(1，0，－)，BC＝(－1，，0)，MN＝(1，0，0)，NP＝. 设平面ABC的一个法向量n1＝(x1，y1，z1)， 由得即 从而 取z1＝1，则x1＝，y1＝1，所以n1＝(，1，1)． 设平面MNP的一个法向量n2＝(x2，y2，z2)，由， 得 即 从而 取z2＝1，则y2＝1，x2＝0，所以n2＝(0，1，1)． 设二面角A ­ NP ­ M的大小为θ，则cos θ＝＝＝. 故二面角A­NP­M的余弦值是.