早教吧作业答案频道 -->数学-->
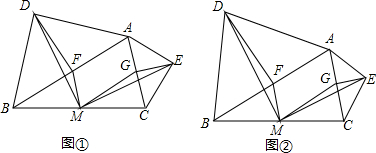
(1)问题发现:如图①,在△ABC中,分别以AB、AC为斜边,向△ABC的形外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点.则①四边形AFMG的形状是②△DFM和
题目详情
(1)问题发现:如图①,在△ABC中,分别以AB、AC为斜边,向△ABC的形外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点.
则①四边形AFMG的形状是___
②△DFM和△MGE之间的关系是___
(2)拓展探究:如图②,在△ABC中,分别以AB、AC为底边,向△ABC的形外作等腰三角形,顶角的顶点分别为D、E,且∠BAD+∠CAE=90°.点F、M、G分别为AB、BC、AC边的中点,
①试判断△DEF和△MGE之间的关系,并加以说明.
②若AD=5,AB=6,△DFM的面积为32,求△MGE的面积.
则①四边形AFMG的形状是___
②△DFM和△MGE之间的关系是___
(2)拓展探究:如图②,在△ABC中,分别以AB、AC为底边,向△ABC的形外作等腰三角形,顶角的顶点分别为D、E,且∠BAD+∠CAE=90°.点F、M、G分别为AB、BC、AC边的中点,
①试判断△DEF和△MGE之间的关系,并加以说明.
②若AD=5,AB=6,△DFM的面积为32,求△MGE的面积.

▼优质解答
答案和解析
(1)①∵BF=AF,BM=MC,
∴FM∥AC,同理MG∥AB,
∴四边形AFMG是平行四边形,
②∵∠BDA=90°,DF是AB边上的中线,
∴DF=AF.
∵四边形AFMG是平行四边形,
∴MG=AF,∠AFM=∠AGM.
∴DF=MG,∠BFM=∠MGC.
∵∠AEC=90°,EG是AC边上的中线,
∴GE=AG.
∵四边形AFMG是平行四边形,
∴AG=FM.
∴GE=FM.
∵DA=DB,F为AB的中点,
∴∠DFB=90°.
同理:∠EGC=90°.
∴∠DFB+∠BFM=∠EGC+∠MGC,即∠DFM=∠EGM.
在△DFM和△MGE中,
,
∴△DFM≌△MGE.
故答案为:①平行四边形;②全等.
(2)①∵△ADB和△ACE都是等腰三角形,且F、G为AB、AC的中点,
∴∠DFB=∠EGC=90°.
∵点F、M、G分别为AB、BC、AC边的中点,
∴FM∥AC,MG∥AB,FM=
AC=AG,MG=
AB=AF.
∴∠BFM=∠BAC=∠MGC.
∴∠BFM+90°=∠MGC+90°,即∠DFM=∠MGE.
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
∴tan∠1=tan∠3.
∴
=
,即
=
.
又∵∠DFM=∠MGE,
∴△DFM∽△MGE.
②∵AD=5,AB=6,
∴AF=3,MG=3,MG=AF=3.
∴在Rt△ADF中,DF=
=
=4.
∵由①知△DFM∽△MGE,且△DFM的面积为32,
∴
=(
)2=(
)2=
.
∴S△MGE=32×
=18.
∴FM∥AC,同理MG∥AB,
∴四边形AFMG是平行四边形,
②∵∠BDA=90°,DF是AB边上的中线,
∴DF=AF.
∵四边形AFMG是平行四边形,
∴MG=AF,∠AFM=∠AGM.
∴DF=MG,∠BFM=∠MGC.
∵∠AEC=90°,EG是AC边上的中线,
∴GE=AG.
∵四边形AFMG是平行四边形,
∴AG=FM.
∴GE=FM.
∵DA=DB,F为AB的中点,
∴∠DFB=90°.
同理:∠EGC=90°.
∴∠DFB+∠BFM=∠EGC+∠MGC,即∠DFM=∠EGM.
在△DFM和△MGE中,
|
∴△DFM≌△MGE.
故答案为:①平行四边形;②全等.
(2)①∵△ADB和△ACE都是等腰三角形,且F、G为AB、AC的中点,
∴∠DFB=∠EGC=90°.
∵点F、M、G分别为AB、BC、AC边的中点,
∴FM∥AC,MG∥AB,FM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BFM=∠BAC=∠MGC.
∴∠BFM+90°=∠MGC+90°,即∠DFM=∠MGE.
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
∴tan∠1=tan∠3.
∴
| DF |
| AF |
| AG |
| GE |
| DF |
| MG |
| FM |
| GE |
又∵∠DFM=∠MGE,
∴△DFM∽△MGE.
②∵AD=5,AB=6,
∴AF=3,MG=3,MG=AF=3.
∴在Rt△ADF中,DF=
| AD2-AF2 |
| 52-32 |
∵由①知△DFM∽△MGE,且△DFM的面积为32,
∴
| S△MGE |
| S△DFM |
| MG |
| DF |
| 3 |
| 4 |
| 9 |
| 16 |
∴S△MGE=32×
| 9 |
| 16 |
看了 (1)问题发现:如图①,在△...的网友还看了以下:
小状元好乘4等于好元状小分别求小状元好各是多少? 2020-03-30 …
褶皱山脉和块状山脉的区别什么是褶皱山,什么是块状山,怎么分别呢,分别有什么代表那块状山呢,是怎样形成 2020-03-31 …
如图是屈肘时肌肉的协作示意图.请据图回答:(1)当屈肘时,以1和2为主的肌群分别处于状态;(2)当 2020-06-17 …
观察与思考图中的石块明显经过加工,分别呈斧状和凿状,可以当作工具,用来砍砸和削刮物体.由此可以推测 2020-06-19 …
朋友在吗.又遇到句子成分的难题了.请帮我分析一下.分别划分出主语,谓语,宾语,状语,补语.也就是句子 2020-11-17 …
在图幅大小相同、比例尺不同的两幅地图中,同一个城市可分别用点状和面状两种符号表示.据图1回答第1题。 2020-11-27 …
在图幅大小相同、比例尺不同的两幅地图中,同一个城市可分别用点状和面状两种符号表示.据图判断,下列说法 2020-11-27 …
状语从句引导在句中成分,状语从句貌似和别的从句不一样?状语从句也是一个句子为什么引导词在句中不做成分 2020-11-28 …
小麦植株无性别之分,品种有抗锈病和不抗锈病、有芒和无芒,控制这两对性状的基因分别位于不同对的染色体上 2020-12-20 …
下面的图形,分别按形状和颜色分类整理并填表.形状合计圆三角形平行四边形个数颜色合计白色灰色黑色个数 2021-01-13 …