早教吧作业答案频道 -->数学-->
如图，将△ABC沿着它的中位线DE对折，点A落在F处．若∠C=120°，∠A=20°，则∠FEB的度数是（）A、140°B、120°C、100°D、80°
题目详情
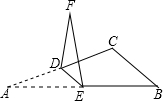如图，将△ABC沿着它的中位线DE对折，点A落在F处．若∠C=120°，∠A=20°，则∠FEB的度数是（ ）| A、140° | B、120° |
| C、100° | D、80° |
▼优质解答
答案和解析
考点：
三角形中位线定理 翻折变换（折叠问题）
专题：
分析：
根据三角形的内角和定理易求∠B的度数，由三角形的中位线定理可得DE∥BC，所以∠B+∠FEB=180°，进而可求出∠FEB的度数．
∵DE是△ABC中位线，∴DE∥BC，∴∠B+∠FEB=180°，∵∠C=120°，∠A=20°，∴∠B=40°，∴∠FEB=140°，故选A．
点评：
本题考查了三角形中位线定理的运用、三角形内角和定理的运用以及平行线的性质，题目的综合性较强，难度一般．
考点：
三角形中位线定理 翻折变换（折叠问题）
专题：
分析：
根据三角形的内角和定理易求∠B的度数，由三角形的中位线定理可得DE∥BC，所以∠B+∠FEB=180°，进而可求出∠FEB的度数．
∵DE是△ABC中位线，∴DE∥BC，∴∠B+∠FEB=180°，∵∠C=120°，∠A=20°，∴∠B=40°，∴∠FEB=140°，故选A．
点评：
本题考查了三角形中位线定理的运用、三角形内角和定理的运用以及平行线的性质，题目的综合性较强，难度一般．
看了 如图，将△ABC沿着它的中位...的网友还看了以下：
集合A={y∈R|y=2x}，B={-1，0，1}，则下列结论正确的是（）A.A∩B={0，1}B. 2020-03-30 …
已知椭圆y^2/a^2+x^2/b^2=1(a>b>0)的右顶点为A(1,0)过其焦点且垂直长轴的 2020-04-06 …
则方程x^2-3x+b=0的两根之和为3,而Q=｛-4,-1,1｝中任意两数之和都不为3,所以P不 2020-05-12 …
已知集合M={3，log2a}，N={a，b}，若M∩N={0}，则M∪N=（）A.{0，1，2} 2020-05-13 …
二次函数f（x）=ax2+2bx+1（a≠0）．（1）若a∈{-2，-1，2，3}，b∈{0，1， 2020-05-13 …
已知椭圆C:x2/a2+y2/b2=1(a>b>0)的离心率e=根号3/2,A(a,0)B(0,b 2020-05-15 …
如图1,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+ 2020-05-16 …
直线y=kx+b,经过a(-1,1)和b(-根号7,0)两点,则不等式-x>kx+b>0的阶级为_ 2020-05-16 …
圆椎曲线双曲线x平方/a平方+y平方/b平方=1(a>1,b>0)的焦距为2c,直线l过点(a,0 2020-05-17 …
已知椭圆x^2/a^2+y^2/b^2=1(a>0,b>0),过点A(a,0)B(b,0)的直线倾 2020-06-23 …