在小学，我们已经初步了解到，正方形的每个角都是90°，每条边都相等．如图，在正方形ABCD外侧作直线AQ，且∠QAD=30°，点D关于直线AQ的对称点为E，连接DE、BE，DE交AQ于点G，BE交AQ于点F．（

Question

在小学，我们已经初步了解到，正方形的每个角都是90°，每条边都相等．如图，在正方形ABCD外侧作直线AQ，且∠QAD=30°，点D关于直线AQ的对称点为E，连接DE、BE，DE交AQ于点G，BE交AQ于点F．

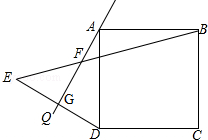
（1）求∠ABE的度数；
（2）若AB=6，求FG的长．

Answer 1

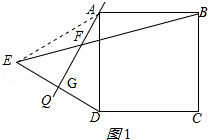（1）连接AE，如图1所示：
∵点D关于直线AQ的对称点为E，
∴AE=AD，AQ垂直平分DE，
∴∠EAQ=∠QAD=30°，
∵四边形ABCD是正方形，
∴∠BAD=90°，AB=AD，
∴AE=AB，
∴∠BAE=30°+30°+90°=150°，
∴∠ABE=(1)/(2)（180°-150°）=15°；  
（2）由（1）得：AE=AD，∠EAD=60°，
∴△AED是等边三角形，ED=6，
∵AQ垂直平分DE，
∴EG=3，∠FGE=90°，
∵∠EAD=30°，∠AEB=15°，
∴∠EFG=∠FEG=45°，
∴EG=FG=3．