早教吧作业答案频道 -->数学-->
点O在△ABC的内部,点D,E,F,G分别是AB,OB,OC,AC的中点.(1)如图1,求证:四边形DEFG是平行四边形;(2)如图2,射线AO交BC边于点H,连接DH,GH,若AB=AC,DE⊥EF,在不添加任何辅助线的
题目详情
点O在△ABC的内部,点D,E,F,G分别是AB,OB,OC,AC的中点.
(1)如图1,求证:四边形DEFG是平行四边形;
(2)如图2,射线AO交BC边于点H,连接DH,GH,若AB=AC,DE⊥EF,在不添加任何辅助线的情况下,请直接写出图2中所有的等腰三角形(不包含以∠BAC为内角的三角形).
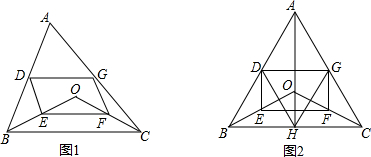
(1)如图1,求证:四边形DEFG是平行四边形;
(2)如图2,射线AO交BC边于点H,连接DH,GH,若AB=AC,DE⊥EF,在不添加任何辅助线的情况下,请直接写出图2中所有的等腰三角形(不包含以∠BAC为内角的三角形).

▼优质解答
答案和解析
(1)证明:如图1中,
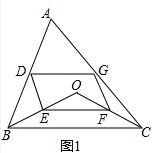
∵AD=DB,AG=GC,
∴DG∥BC,DG=
BC,
∵OE=EB,OF=FC,
∴EF∥BC,EF=
BC,
∴DG∥EF,EF=DG,
∴四边形DEFG是平行四边形.
(2)如图2中,
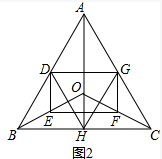
∵BD=DA,BE=EO,
∴DE∥AO,
∵EF∥BC,DE⊥EF,
∴DE⊥BC,
∴AH⊥BC,
∵AB=AC,
∴BH=HC,
∴OB=OC,OE=OF,
∴△OBC,△OEF是等腰三角形,
∵DH是RT△ABH斜边中线,
∴DH=BD=AD,
∴△BDH,△DHA是等腰三角形,同理△HGC,△HGA都是等腰三角形.
综上所述等腰三角形有△OBC,△OEF,△HGC,△HGA,△BDH,△DHA.

∵AD=DB,AG=GC,
∴DG∥BC,DG=
| 1 |
| 2 |
∵OE=EB,OF=FC,
∴EF∥BC,EF=
| 1 |
| 2 |
∴DG∥EF,EF=DG,
∴四边形DEFG是平行四边形.
(2)如图2中,

∵BD=DA,BE=EO,
∴DE∥AO,
∵EF∥BC,DE⊥EF,
∴DE⊥BC,
∴AH⊥BC,
∵AB=AC,
∴BH=HC,
∴OB=OC,OE=OF,
∴△OBC,△OEF是等腰三角形,
∵DH是RT△ABH斜边中线,
∴DH=BD=AD,
∴△BDH,△DHA是等腰三角形,同理△HGC,△HGA都是等腰三角形.
综上所述等腰三角形有△OBC,△OEF,△HGC,△HGA,△BDH,△DHA.
看了 点O在△ABC的内部,点D,...的网友还看了以下:
找规律谢谢帮助!用火柴棒拼正方形第一个图形是1个正方形火柴棒根数是4第二个图形是2个正方形火柴棒根 2020-05-17 …
“形而上‘’的“形”是什么意思 2020-05-23 …
"形而上者谓之道"的“形”是什么意思? 2020-05-23 …
三角形里有一个圆是几?一个圆圈在正方形里是3,圆圈里一个正方形是1,正方形里一个三角形是6,三角形 2020-06-12 …
《陋室铭》中无案牍之劳形的形是什么意思? 2020-06-18 …
“无案牍之劳形”中的“形”是什么意思?快 2020-06-18 …
形影不离的形是什么意思?只要“形”的意思! 2020-06-18 …
归而形诸梦的形是什么意思RT 2020-12-15 …
这样的形是不是平行四边形一个四边形中,一组对边相等,一条对角线被另一对角线平分,它是不是平行四边形, 2020-12-25 …
古都的秋本文的形是什么神是什么形神的结合点是什么 2020-12-25 …