早教吧作业答案频道 -->数学-->
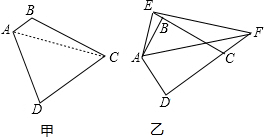
有一个四边形ABCD,BC=CD,∠BCD=60°,∠BAD=120°.(1)小明认为AB+AD=AC(如图甲),为了证明它,需要作辅助线,请问需要怎样作辅助线?小明认为作完辅助线后,还要证明一对三角形全等,
题目详情
有一个四边形ABCD,BC=CD,∠BCD=60°,∠BAD=120°.
(1)小明认为AB+AD=AC(如图甲),为了证明它,需要作辅助线,请问需要怎样作辅助线?小明认为作完辅助线后,还要证明一对三角形全等,请指出这一对三角形;
(2)若AB=AD(如图乙),F是DC延长线上一点,作∠FAE=60°,AE与CB的延长线交点为E,连EF,线段EF、EB和DF之间有怎样的数量关系?请说明理由.
(1)小明认为AB+AD=AC(如图甲),为了证明它,需要作辅助线,请问需要怎样作辅助线?小明认为作完辅助线后,还要证明一对三角形全等,请指出这一对三角形;
(2)若AB=AD(如图乙),F是DC延长线上一点,作∠FAE=60°,AE与CB的延长线交点为E,连EF,线段EF、EB和DF之间有怎样的数量关系?请说明理由.

▼优质解答
答案和解析
(1)△BDG≌△CDA;
如图甲,
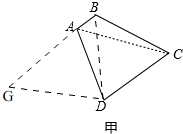
连接BD,延长BA至G,使AG=AD,
∵∠BAD=120°,
∴∠DAG=60°,
∵AG=AD,
∴△ADG是等边三角形,
∴∠ADG=60°,DG=AD,
∵∠BCD=60°,BC=CD,
∴△BCD是等边三角形,
∴∠BDC=60°,BD=CD,
∴∠BDG=∠CDA,
在△BDG和△CDA中,
,
∴△BDG≌△CDA,
∴AC=BG=AG+AB=AD+AB,
(2)DF=EB+EF,
理由:如图乙,
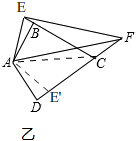
在四边形ABCD中,∠BAD=120°∠BCD=60°,
根据四边形的内角和得,∠ABC+∠ADC=180°
在△ABC和△ADC中,
,
∴△ABC≌△ADC,
∴∠ABC=∠ADC=90°,∠BAC=∠DAC=60°,
∵∠EAF=60°,
∴∠EAB=∠CAF
在△ACD内部作∠DAE'=∠BAE,
∴∠CAF=∠DAE',
∴∠FAE'=∠FAC+∠CAE'=∠DAE'+∠CAE'=60°=∠EAF,
在△ADE'和△ABE中,
,
∴△ADE'≌△ABE,
∴AE'=AE,
在△EAF和△E'AF中,
,
∴△EAF≌△E'AF,
∴EF=E'F,
∴DF=DE'+E'F=EB+EF.
如图甲,

连接BD,延长BA至G,使AG=AD,
∵∠BAD=120°,
∴∠DAG=60°,
∵AG=AD,
∴△ADG是等边三角形,
∴∠ADG=60°,DG=AD,
∵∠BCD=60°,BC=CD,
∴△BCD是等边三角形,
∴∠BDC=60°,BD=CD,
∴∠BDG=∠CDA,
在△BDG和△CDA中,
|
∴△BDG≌△CDA,
∴AC=BG=AG+AB=AD+AB,
(2)DF=EB+EF,
理由:如图乙,

在四边形ABCD中,∠BAD=120°∠BCD=60°,
根据四边形的内角和得,∠ABC+∠ADC=180°
在△ABC和△ADC中,
|
∴△ABC≌△ADC,
∴∠ABC=∠ADC=90°,∠BAC=∠DAC=60°,
∵∠EAF=60°,
∴∠EAB=∠CAF
在△ACD内部作∠DAE'=∠BAE,
∴∠CAF=∠DAE',
∴∠FAE'=∠FAC+∠CAE'=∠DAE'+∠CAE'=60°=∠EAF,
在△ADE'和△ABE中,
|
∴△ADE'≌△ABE,
∴AE'=AE,
在△EAF和△E'AF中,
|
∴△EAF≌△E'AF,
∴EF=E'F,
∴DF=DE'+E'F=EB+EF.
看了 有一个四边形ABCD,BC=...的网友还看了以下:
(2分)在一元强碱MOH溶液中加入一元酸HA溶液,充分反应后,溶液呈中性。甲同学认为溶液中c(A- 2020-05-13 …
有关甲醛分子的说法正确的是()A.C原子采用sp杂化B.甲醛分子为三角锥结构C.甲醛分子为三角 2020-05-14 …
田径场上正在进行100米决赛.参加决赛的是A、B、C、D、E、F六个人.关于谁会得冠军,看台上甲、 2020-05-16 …
甲认为柴油机输油泵的供油量可以调整,乙认为不可以,你认为( )对。A.甲B.乙C.甲和乙D.其他 2020-05-31 …
甲欲杀乙,误将丙当乙杀死,甲的行为属于事实上的认识错误之()。A.目标的错误认识B.手段的错误认识C 2020-06-04 …
下列纠纷中,不适用《仲裁法》解决的有().A.甲乙之间的土地承包合同纠纷B.甲乙之间的货物买卖合同 2020-06-17 …
某地区水电站规定,如果每月用电不超过24度,则每度收9分钱,如果超过24度,则多出度数按每度2角收 2020-06-18 …
甲醛(H2C=O)在Ni催化作用下加氢可得甲醇(CH3OH),以下说法中不正确的是()A.甲醇分子 2020-07-07 …
设甲:角X是第一象限角,乙:角X是锐角,则A,甲是乙的充分条件,但不是乙的必要条件B,甲是乙的必要 2020-08-03 …
下列行为属于正当防卫的是A.甲和乙打架,被打伤的乙将在旁围观的甲的小孩打伤B.甲偷了乙的自行车,乙发 2020-12-10 …