早教吧作业答案频道 -->数学-->
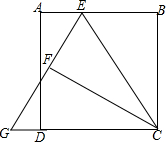
如图,矩形ABCD中,BC=3,且BC>AB,E为AB边上任意一点(不与A,B重合),设BE=t,将△BCE沿CE对折,得到△FCE,延长EF交CD的延长线于点G,则tan∠CGE=(用含t的代数式表示).
题目详情
如图,矩形ABCD中,BC=3,且BC>AB,E为AB边上任意一点(不与A,B重合),设BE=t,将△BCE沿CE对折,得到△FCE,延长EF交CD的延长线于点G,则tan∠CGE=___(用含t的代数式表示).

▼优质解答
答案和解析
如图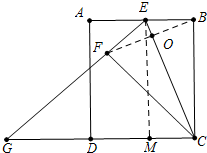 连接BF交EC于O,作EM⊥CD于M,
连接BF交EC于O,作EM⊥CD于M,
∵∠EMC=∠EBC=∠BCM=90°,
∴四边形EBCM是矩形,
∴CM=EB=t,EM=BC=3,
在RT△EBC中,∵EB=t,BC=3,
∴EC=
=
,
∵EB=EF,CB=CF,
∴EC垂直平分BF,
∵
•EC•BO=
•EB•BC,
∴BO=
,BF=2BO=
∵∠AEF+∠BEF=180°,∠BEF+∠BCF=180°,
∴∠AEF=∠BCF,
∵AB∥CD,
∴∠BEC=∠ECG=∠CEF,∠AEF=∠G=∠BCF
∴GE=GC,
∴∠GCE=∠GEC=∠CFB=∠CBF,
∴△CBF∽△GCE,
∴
=
,
∴GC=
,GM=GC-CM=
,
∴tan∠CGE=
=
.
故答案为
.
 连接BF交EC于O,作EM⊥CD于M,
连接BF交EC于O,作EM⊥CD于M,∵∠EMC=∠EBC=∠BCM=90°,
∴四边形EBCM是矩形,
∴CM=EB=t,EM=BC=3,
在RT△EBC中,∵EB=t,BC=3,
∴EC=
| t2+32 |
| t2+9 |
∵EB=EF,CB=CF,
∴EC垂直平分BF,
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴BO=
| 3t | ||
|
| 6t | ||
|
∵∠AEF+∠BEF=180°,∠BEF+∠BCF=180°,
∴∠AEF=∠BCF,
∵AB∥CD,
∴∠BEC=∠ECG=∠CEF,∠AEF=∠G=∠BCF
∴GE=GC,
∴∠GCE=∠GEC=∠CFB=∠CBF,
∴△CBF∽△GCE,
∴
| GC |
| BC |
| EC |
| BF |
∴GC=
| t2+9 |
| 2t |
| 9-t2 |
| 2t |
∴tan∠CGE=
| EM |
| GM |
| 6t |
| 9-t2 |
故答案为
| 6t |
| 9-t2 |
看了 如图,矩形ABCD中,BC=...的网友还看了以下:
-Theyusedtobegoodfriendsbutnowthearelikestrangers 2020-05-13 …
阅读以下四篇短文,请根据要求作答。A篇根据短文内容,判断下列句子,正确的用“A”,错误的用“B”。 2020-05-14 …
下列理解,不符合原文意思的一项是()A.《诗经》里出现的啸者多是女性,在记载中常常提及的妇女作啸大 2020-05-15 …
如何分析“Anointmentismadefromtheingredientthatmakesch 2020-06-06 …
enrolment和enrollment请问enrolment和enrollment这两个词的用法 2020-06-14 …
1.老人引杨氏入山之大穴2.与众共之3.杨谢而从之3个“之”的用法含义 2020-07-08 …
对人粪尿要进行处理,是因为人粪尿()A.不能为植物所利用B.含有大量的病菌、虫卵和其它有害质C.不 2020-07-16 …
下列有关盐类水解的叙述中正确的是()A.溶液呈中性的盐一定是强酸、强碱生成的盐B.含有弱酸根盐的水 2020-07-25 …
请详细地说出another,other,others,theother的用法,含义,区别等. 2020-07-26 …
英文单词yet的用法含意Thisistoensurethatthephotofileissmally 2020-12-02 …