早教吧作业答案频道 -->数学-->
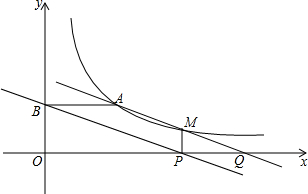
如图,点A(3,2)和点M(m,n)都在反比例函数y=kx(x>0)的图象上.(1)求k的值,并求当m=4时,直线AM的解析式;(2)过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴
题目详情
如图,点A(3,2)和点M(m,n)都在反比例函数y=
(x>0)的图象上.
(1)求k的值,并求当m=4时,直线AM的解析式;
(2)过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴于点Q,试说明四边形ABPQ是平行四边形;
(3)在(2)的条件下,四边形ABPQ能否为菱形?若能,请求出m的值;若不是,请说明理由.
| k |
| x |

(1)求k的值,并求当m=4时,直线AM的解析式;
(2)过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴于点Q,试说明四边形ABPQ是平行四边形;
(3)在(2)的条件下,四边形ABPQ能否为菱形?若能,请求出m的值;若不是,请说明理由.
▼优质解答
答案和解析
(1)把A(3,2)代入得:k=6,
∴反比例函数的解析式为:y=
;
把m=4代入反比例解析式得:n=
=1.5,
∴M(4,1.5),
设直线AM的解析式为:y=kx+b;
根据题意得:
,
解得:k=-0.5,b=3.5,
∴直线AM的解析式为:y=-0.5x+3.5;
(2)根据题意得:P(m,0),M(m,
),B(0,2),
设直线BP的解析式为:y=kx+b,
把点B(0,2),P(m,0)代入得:
,
解得:k=-
;
设直线AM的解析式为:y=ax+c,
把点A(3,2),M(m,
)代入得:
,
解得a=-
,
∵k=a=-
,
∴直线BP与直线AM的位置关系是BP∥AM,
∵AB∥PQ,
∴四边形ABPQ是平行四边形;
(3)在(2)的条件下,四边形ABPQ能为菱形,理由为:
若四边形ABPQ为菱形,则有AB=BP=3,
∴m2+22=9,即m2=5,
此时m=
,
则在(2)的条件下,四边形ABPQ能为菱形.
∴反比例函数的解析式为:y=
| 6 |
| x |
把m=4代入反比例解析式得:n=
| 6 |
| 4 |
∴M(4,1.5),
设直线AM的解析式为:y=kx+b;
根据题意得:
|
解得:k=-0.5,b=3.5,
∴直线AM的解析式为:y=-0.5x+3.5;
(2)根据题意得:P(m,0),M(m,
| 6 |
| m |
设直线BP的解析式为:y=kx+b,
把点B(0,2),P(m,0)代入得:
|
解得:k=-
| 2 |
| m |
设直线AM的解析式为:y=ax+c,
把点A(3,2),M(m,
| 6 |
| m |
|
解得a=-
| 2 |
| m |
∵k=a=-
| 2 |
| m |
∴直线BP与直线AM的位置关系是BP∥AM,
∵AB∥PQ,
∴四边形ABPQ是平行四边形;
(3)在(2)的条件下,四边形ABPQ能为菱形,理由为:
若四边形ABPQ为菱形,则有AB=BP=3,
∴m2+22=9,即m2=5,
此时m=
| 5 |
则在(2)的条件下,四边形ABPQ能为菱形.
看了 如图,点A(3,2)和点M(...的网友还看了以下:
为了解和推算全国城乡居民的消费支出结构,统计应采取的调查方式是()。A.普查B.重点调查C.典型调查 2020-05-21 …
国内邮件按性质分为函件和( )。A.平常邮件B.信件C.包件D.快件 2020-05-31 …
二元一次与一次函数的知识点解答以方程X+Y=3的解为坐标组成的图形就是一次函数的图像二元一次方程的 2020-06-03 …
相对论中那种“可弯曲的网”的模型是爱因斯坦想出来的还是后人为理解和解释而建立的? 2020-06-05 …
函数可否看作是特殊的方程因为函数和方程指尖的关系. 2020-06-12 …
如图,反比例函数y1=k/x与一次函数y2=ax+b的图象相交与A(3,1)和B(-1,m)(1) 2020-06-27 …
中性酸根是什么?碱式酸根和酸式酸根又分别是什么?帮忙说明下,最好再多举几个例子,到底是怎么回事啊? 2020-07-24 …
抓住关键词是为了解和掌握历史知识的方法之一.与“农业生产合作社”“公私合营”“社会主义基本制度建立” 2020-12-01 …
百善孝为先,要做到孝敬父母和长辈我们必须()①敬重和爱戴父母②宽恕父母的不道德行为③理解和关心父母④ 2020-12-05 …
莫高窟俗称千佛洞,被誉为20世纪最有价值的文化发现、“东方卢浮宫”。1987年,敦煌莫高窟入选《世界 2020-12-22 …