早教吧作业答案频道 -->数学-->
如图,抛物线y=x2+bx+c与x轴交A(-1,0)B(3,0)两点,直线l与抛物线交于A,C两点,其中C点的横坐标为2.(1)求抛物线的解析式;(2)求直线AC的函数表达式;(3)若点M是线段AC上的点(
题目详情
如图,抛物线y=x2+bx+c与x轴交A(-1,0)B(3,0)两点,直线l与抛物线交于A,C两点,其中C点的横坐标为2.
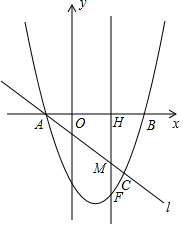
(1)求抛物线的解析式;
(2)求直线AC的函数表达式;
(3)若点M是线段AC上的点(不与A,C重合),过M作MF∥y轴交抛物线于F,交x轴于点H,设点M的横坐标为m,连接FA,FC,是否存在m,使△AFC的面积最大?若存在,求m的值;若不存在,说明理由.

(1)求抛物线的解析式;
(2)求直线AC的函数表达式;
(3)若点M是线段AC上的点(不与A,C重合),过M作MF∥y轴交抛物线于F,交x轴于点H,设点M的横坐标为m,连接FA,FC,是否存在m,使△AFC的面积最大?若存在,求m的值;若不存在,说明理由.
▼优质解答
答案和解析
(1)把A(-1,0),B(3,0)代入y=x2+bx-c,可得
,解得
,
∴抛物线解析式为y=x2-2x-3;
(2)把x=2代入抛物线解析式可得y=22-2×2-3=-3,
∴C(2,-3),
设直线AC的解析式为y=kx+s,把A、C坐标代入可得,
,解得
,
∴直线AC解析式为y=-x-1;
(3)存在m,使△AFC的面积最大.
理由如下:
∵点M在直线AC上,
∴M(m,-m-1),
∵点F在抛物线上,
∴F(m,m2-2m-3),
∵点M是线段AC上的点,
∴MF=(-m-1)-(m2-2m-3)=-m2+m+2,
∵A(-1,0),C(2,-3),
∴S△ACF=
MF•[2-(-1)]=
MF=
(-m2+m+2)=-
(m-
)2+
,
∵-
<0,
∴当m=
时,△AFC的面积最大,最大为值为
.
(1)把A(-1,0),B(3,0)代入y=x2+bx-c,可得
|
|
∴抛物线解析式为y=x2-2x-3;
(2)把x=2代入抛物线解析式可得y=22-2×2-3=-3,
∴C(2,-3),
设直线AC的解析式为y=kx+s,把A、C坐标代入可得,
|
|
∴直线AC解析式为y=-x-1;
(3)存在m,使△AFC的面积最大.
理由如下:
∵点M在直线AC上,
∴M(m,-m-1),
∵点F在抛物线上,
∴F(m,m2-2m-3),
∵点M是线段AC上的点,
∴MF=(-m-1)-(m2-2m-3)=-m2+m+2,
∵A(-1,0),C(2,-3),
∴S△ACF=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 27 |
| 8 |
∵-
| 3 |
| 2 |
∴当m=
| 1 |
| 2 |
| 27 |
| 8 |
看了 如图,抛物线y=x2+bx+...的网友还看了以下:
图中构成东西半球分界线的两条经线是()A.A线和C线B.A线和D线C.B线和C线D.B线和D线 2020-04-23 …
读世界海陆分布图,回答5~6题图中构成东西半球分界线的经线是()A.A线和C线B.A线和D线C.B 2020-04-23 …
图中构成东西半球分界线的两条经线是()A.A线和C线B.A线和D线C.B线和C线D.B线和D线 2020-04-23 …
图中构成东西半球分界线的两条经线是()A.A线和C线B.A线和D线C.B线和C线D.B线和D线 2020-04-23 …
读世界七大洲分布图,回答4-7题.图中构成东西半球分界线的两条经线是()A.A线和C线B.A线和D 2020-04-23 …
一张白纸上有三条直线,已知直线a平行于直线b,直线b平行于直线c,且直线a与直线b之间的距离为3厘 2020-06-19 …
一张白纸上有三条直线,已知直线a平行于直线b,直线b平行于直线c且直线a与直线b之间的距离为3厘米 2020-07-22 …
已知直线a.b是异面直线,直线c.d分别与ab都相交,求直线cd的位置关系()a.可能已知直线a. 2020-08-02 …
已知a,b是异面直线,直线c∥直线a,则c与b的位置关系是()已知a,b是异面直线,直线c∥直线a 2020-08-02 …
读图完成第4~5小题.图中构成东西半球分界线的两条经线是()A.A线和C线B.A线和D线C.B线和C 2020-12-21 …