早教吧作业答案频道 -->数学-->
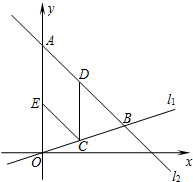
如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).(1)求直线l1,l2的表达式.(2)点C为线段OB上一动点(点C不与
题目详情
如图,在平面直角坐标系内,点A的坐标为(0,24 ),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
(1)求直线l1,l2的表达式.
(2)点C为线段OB上一动点(点C不与点O,B重合),CD∥y轴交直线l2于点D,CE∥l2交y轴于点E.
①若点C的横坐标为m,求四边形AECD的面积S与m的函数关系式;
②当S最大时,求出点C的坐标.

(1)求直线l1,l2的表达式.
(2)点C为线段OB上一动点(点C不与点O,B重合),CD∥y轴交直线l2于点D,CE∥l2交y轴于点E.
①若点C的横坐标为m,求四边形AECD的面积S与m的函数关系式;
②当S最大时,求出点C的坐标.
▼优质解答
答案和解析
(1)设直线l1的表达式为y=k1x,
将点B(18,6)代入y=k1x中得:18k1=6,
解得:k1=
,
∴直线l1的表达式为y=
x.
设直线l2的表达式为y=k2x+b,
将点A(0,24),B(18,6)代入y=k2x+b中得:
,
解得:
,
∴直线l2的表达式为y=-x+24.
(2)①将x=m代入y=
x得:y=
m,
∴点C的坐标为(m,
m)(0<m<18).
∵CD∥y轴,
∴D点的横坐标也为m,
将x=m代入y=-x+24中得:y=-m+24,
∴点D的坐标为(m,-m+24),
∴CD=(-m+24)-
m=-
m+24.
∵CD∥y轴,CE∥l2,
∴四边形AECD为平行四边形.
∵C(m,
m),
∴CD边上的高为m,
∴S=(-
m+24)m=-
m2+24m(0<m<18).
②由S=-
m2+24m得:-
=9,
∴当m=9时,S最大,
此时
m=3.
∴当S最大时,点C的坐标为(9,3).
将点B(18,6)代入y=k1x中得:18k1=6,
解得:k1=
| 1 |
| 3 |
∴直线l1的表达式为y=
| 1 |
| 3 |
设直线l2的表达式为y=k2x+b,
将点A(0,24),B(18,6)代入y=k2x+b中得:
|
解得:
|
∴直线l2的表达式为y=-x+24.
(2)①将x=m代入y=
| 1 |
| 3 |
| 1 |
| 3 |
∴点C的坐标为(m,
| 1 |
| 3 |
∵CD∥y轴,
∴D点的横坐标也为m,
将x=m代入y=-x+24中得:y=-m+24,
∴点D的坐标为(m,-m+24),
∴CD=(-m+24)-
| 1 |
| 3 |
| 4 |
| 3 |
∵CD∥y轴,CE∥l2,
∴四边形AECD为平行四边形.
∵C(m,
| 1 |
| 3 |
∴CD边上的高为m,
∴S=(-
| 4 |
| 3 |
| 4 |
| 3 |
②由S=-
| 4 |
| 3 |
| b |
| 2a |
∴当m=9时,S最大,
此时
| 1 |
| 3 |
∴当S最大时,点C的坐标为(9,3).
看了 如图,在平面直角坐标系内,点...的网友还看了以下:
在锐角△ABC中,a.b.c分别为角A.B.C所对的边,又c=√21b=4且BC边上的高h=2√3. 2020-03-30 …
什么是斜三角形设A={x│x是锐角三角形},B={x│x是钝角三角形},求A∩B 2020-05-14 …
在直角三角形ABC中,∠C=90度,AB的中垂线交AC于点D,交AB于点E,BD平分角ABC,求∠ 2020-06-05 …
集合A={xIx>-1},B{xIx≥2}求A并B集合A={xIx是锐角三角形},B{xIx是钝角 2020-06-08 …
在三角形abc中角,角a+角b等于100度,角c等于2角b求a、b、c度数 2020-07-22 …
A是等腰三角形,B是直角三角形,求A交B我已经知道答案,谁是谁的子集啊?如果是等腰直角三角形,那不 2020-07-30 …
已知A=集合X是等腰三角形,B=集合X是直角三角形,求A并B和A交B已知A=集合X是等腰三角形,B 2020-07-30 …
1.已知集合A={x/x为锐角三角形},B={x/x为钝角三角形},求A交B,AUB.2.已知A= 2020-08-02 …
一个集合问题!A{x|x是锐角三角形}B(x|x是钝角三角形)求A交BA交B=空集还是A交B={空 2020-08-02 …
三角形求a+b的取值范围为什么不能用基本不等式在锐角三角形ABC中,c=根号6,C=60度,求a+ 2020-08-02 …