早教吧作业答案频道 -->数学-->
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.(Ⅰ)求证:AE⊥BD';(Ⅱ)求三棱锥A-BCD'的体积.
题目详情
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.
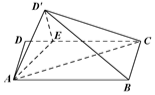
(Ⅰ)求证:AE⊥BD';
(Ⅱ)求三棱锥A-BCD'的体积.

(Ⅰ)求证:AE⊥BD';
(Ⅱ)求三棱锥A-BCD'的体积.
▼优质解答
答案和解析
证明:(Ⅰ)连接BD交AE于点O,依题意得
=
=2,
所以Rt△ABD~Rt△DAE,
所以∠DAE=∠ABD,所以∠AOD=90°,所以AE⊥BD,
即OB⊥AE,OD'⊥AE,又OB∩OD′=O,
OB,OD'⊂平面OBD'.
所以AE⊥平面OBD'.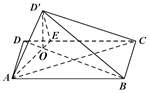
(Ⅱ)因为平面AD'E⊥平面ABCE,
由(Ⅰ)知,OD'⊥平面ABCE,
所以OD'为三棱锥D'-ABC的高,
在矩形ABCD中,AB=4,AD=2,DE=1,所以D′O=
,
所以VA-BCD'=VD'-ABC=
S△ABC•D′O=
×(
×4×2)×
=
即三棱锥A-BCD'的体积为
.
| AB |
| DA |
| AD |
| DE |
所以Rt△ABD~Rt△DAE,
所以∠DAE=∠ABD,所以∠AOD=90°,所以AE⊥BD,
即OB⊥AE,OD'⊥AE,又OB∩OD′=O,
OB,OD'⊂平面OBD'.
所以AE⊥平面OBD'.

(Ⅱ)因为平面AD'E⊥平面ABCE,
由(Ⅰ)知,OD'⊥平面ABCE,
所以OD'为三棱锥D'-ABC的高,
在矩形ABCD中,AB=4,AD=2,DE=1,所以D′O=
| 2 | ||
|
所以VA-BCD'=VD'-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 | ||
|
8
| ||
| 15 |
即三棱锥A-BCD'的体积为
8
| ||
| 15 |
看了 如图,矩形ABCD中,AB=...的网友还看了以下:
.谁把过程发给我.1、分析下列程序,并给出程序运行结果#include”stdio.h”main( 2020-05-15 …
设有关系模式R(A,B,C,D,E,F),若有如下的函数依赖集F={A→B,(C,A)→D, (E, 2020-05-24 …
与逆波兰式“abc*+-d*ef- -”对应的中缀表达式是(27)。A.-(a*b+c-d*e-f) 2020-05-26 …
中缀表达式A-(B+C/D)×E的后缀形式是(41)。A.ABC+D/×E-B.ABCD/+E×-C 2020-05-26 …
设实数a,b,c,d,e满足(a+c)(a+d)=(b+c)(b+d)=e≠O,且a≠b,那么(a 2020-06-08 …
这5道题用波兰式表达(1)A*(B-C)+T/(D+E)-F/(S*H)(2)A/(B*C(E+F 2020-07-08 …
1.在RtA△BC中,∠C=90°.D,E分别是AB,AC的中点,AC=7,BC=4,若以C为圆心 2020-07-26 …
若abcd都是整数,其中c>0,并且满足a+b+c=d,b+c+d=e,c+d+e=a,e+a=b 2020-07-30 …
A+B+C=84,D+E+F=111,H+I+J=138,A+D+H=124,B+E+I=148,C 2020-12-14 …
数据结构将下列各算术运算式表示成波兰式和逆波兰式:(A*(B+C)+D)*E-F*GA*(B-D)+ 2020-12-15 …