早教吧作业答案频道 -->数学-->
如图,ABC-A1B1C1是底面边长为2,高为32的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).(1)证明:PQ∥A1B1;(2)当CF⊥平面ABQP时,在图中作出点C在平面ABQP内的正投
题目详情
如图,ABC-A1B1C1是底面边长为2,高为
的正三棱柱,经过AB的截面与上
底面相交于PQ,设C1P=λC1A1(0<λ<1).
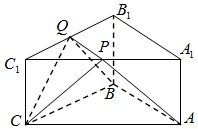
(1)证明:PQ∥A1B1;
(2)当CF⊥平面ABQP时,在图中作出点C在平面ABQP内的正投影F(说明作法及理由),并求四棱锥CABPQ表面积.
| ||
| 2 |
底面相交于PQ,设C1P=λC1A1(0<λ<1).

(1)证明:PQ∥A1B1;
(2)当CF⊥平面ABQP时,在图中作出点C在平面ABQP内的正投影F(说明作法及理由),并求四棱锥CABPQ表面积.
▼优质解答
答案和解析
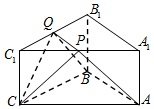 证明:(I)∵平面ABC∥平面A1B1C1,平面ABC∩平面ABQP=AB,
证明:(I)∵平面ABC∥平面A1B1C1,平面ABC∩平面ABQP=AB,
平面ABQP∩平面A1B1C1=QP,
∴AB∥PQ,又∵AB∥A1B1,∴PQ∥A1B1. (5分)
(Ⅱ)F点是PQ中点,理由如下:
当λ=
时,P,Q分别是A1C1,A1B1的中点,
连接CQ和CP,∵ABC-A1B1C1是正三棱柱,
∴CQ=CP,∴CF⊥QP,(6分)
取AB中点H,连接FH,CH,CH=
,
在等腰梯形ABQP中,FH=
,
连接CF,则CF=
,
∴CF2+FH2=CH2,∴CF⊥FH,
∵QP∩FH=H,∴CF⊥平面ABF,即CF⊥平面ABQP,(9分)
∴F点是C在平面ABQP内的正投影.
∴四棱锥CABPQ表面积:
S=S△CPQ+S△CPA+S△CQB+SPQBA+S△ABC=2
+
.(12分)
 证明:(I)∵平面ABC∥平面A1B1C1,平面ABC∩平面ABQP=AB,
证明:(I)∵平面ABC∥平面A1B1C1,平面ABC∩平面ABQP=AB,平面ABQP∩平面A1B1C1=QP,
∴AB∥PQ,又∵AB∥A1B1,∴PQ∥A1B1. (5分)
(Ⅱ)F点是PQ中点,理由如下:
当λ=
| 1 |
| 2 |
连接CQ和CP,∵ABC-A1B1C1是正三棱柱,
∴CQ=CP,∴CF⊥QP,(6分)
取AB中点H,连接FH,CH,CH=
| 3 |
在等腰梯形ABQP中,FH=
| ||
| 2 |
连接CF,则CF=
| ||
| 2 |
∴CF2+FH2=CH2,∴CF⊥FH,
∵QP∩FH=H,∴CF⊥平面ABF,即CF⊥平面ABQP,(9分)
∴F点是C在平面ABQP内的正投影.
∴四棱锥CABPQ表面积:
S=S△CPQ+S△CPA+S△CQB+SPQBA+S△ABC=2
| 3 |
| 6 |
看了 如图,ABC-A1B1C1是...的网友还看了以下:
求长方体表面积时S底=2*(A*B+B*C+A*C)这个公式的各求的是哪个面S底=2*(A*B+B 2020-05-13 …
matlab解中学三角函数方程数学题,不会求大大~~~~~~~~~~[a,b,c,A,B,C]=s 2020-05-14 …
1、已知a,b,c互不相等求2a-b-c/(a-b)(b-c)+2b-c-a/(b-c)(b-a) 2020-05-16 …
分解因式(a-b-c)(a+b-c)-(b-c-a)(b+c-a)正确答案是这个:(a+b-c)( 2020-05-17 …
三棱台ABC-A`B`C`的上下底面均为正三角形三棱台ABC-A'B'C'的上下底面均为正三角形, 2020-05-21 …
1.要画一个三角形,需要知道三个元素,其中至少一个元素是2.三角形的三边长a,b,c,满足b分之a 2020-06-08 …
乘法分配律a*c+b*c=(a+b)*c到底是乘法分配律还是结合律?有的人说是乘法分配律的逆运用, 2020-07-11 …
(a+b+c)^3-(b+c-a)^3-(c+a-b)^3-(a+b-c)^3=[(a+b+c)^ 2020-08-02 …
不等式中循环和∑的定义比方说有3个元a,b,c∑a^2b^3到底是多少(有3项还是6项?)那有a,b 2020-10-31 …
对数函数换底公式1.a^2=c^2-b^2,是怎样推到1/(2log(c-b)a)+1/(2log( 2021-01-07 …