早教吧作业答案频道 -->数学-->
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=2AD,PD⊥底面ABCD,E,F分别为棱AB,PC的中点.(1)求证:EF∥平面PAD;(2)求证:平面PDE⊥平面PEC.
题目详情
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=2AD,PD⊥底面ABCD,E,F分别为棱AB,PC的中点.
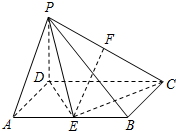
(1)求证:EF∥平面PAD;
(2)求证:平面PDE⊥平面PEC.

(1)求证:EF∥平面PAD;
(2)求证:平面PDE⊥平面PEC.
▼优质解答
答案和解析
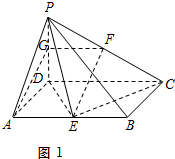 证明:(1)取PD的中点G,连接AG,FG.
证明:(1)取PD的中点G,连接AG,FG.
∵F,G分别是PC,PD的中点,
∴GF∥DC,GF=
DC,
又E是AB的中点,
∴AE∥DC,且AE=
DC,
∴GF∥AE,且GF=AE,
∴四边形AEFG是平行四边形,故EF∥AG.
又EF⊂平面PAD,AG⊄平面PAD,
∴EF∥平面PAD.
(2)∵PD⊥底面ABCD,EC⊂底面ABCD,
∴CE⊥PD.
∵四边形ABCD是矩形,AB=2AD,
∴DE=
AD,CE=
AD,CD=2AD,
∴DE2+CE2=CD2,即CE⊥DE,
又PD⊂平面PDE,DE⊂平面PDE,PD∩DE=D,
∴CE⊥平面PDE.
∵CE⊂平面PEC,
∴平面PDE⊥平面PEC.
 证明:(1)取PD的中点G,连接AG,FG.
证明:(1)取PD的中点G,连接AG,FG.∵F,G分别是PC,PD的中点,
∴GF∥DC,GF=
| 1 |
| 2 |
又E是AB的中点,
∴AE∥DC,且AE=
| 1 |
| 2 |
∴GF∥AE,且GF=AE,
∴四边形AEFG是平行四边形,故EF∥AG.
又EF⊂平面PAD,AG⊄平面PAD,
∴EF∥平面PAD.
(2)∵PD⊥底面ABCD,EC⊂底面ABCD,
∴CE⊥PD.
∵四边形ABCD是矩形,AB=2AD,
∴DE=
| 2 |
| 2 |
∴DE2+CE2=CD2,即CE⊥DE,
又PD⊂平面PDE,DE⊂平面PDE,PD∩DE=D,
∴CE⊥平面PDE.
∵CE⊂平面PEC,
∴平面PDE⊥平面PEC.
看了 如图,四棱锥P-ABCD中,...的网友还看了以下:
一道三角形相似题,如图:F'D’‖FD,F’E’‖FE.△EFD∽△E’F’D’吗? 2020-03-30 …
数据结构-广义表1、广义表A(a,(b,c,(d,e,f),(),g,h,(r,s,t))的长度, 2020-05-14 …
如下表,a、b、c、d、e、f均为有理数,表中各行各列、两条对角线上三个数之和都相等,试计算:(a 2020-05-21 …
如下表,a、b、c、d、e、f均为有理数,表中各行各列、两条对角线上三个数之和都相等、试计算(a+ 2020-05-21 …
一到证明题求解.利用常用永真蕴含公式证明(A→(B→C))∧((C∧D)→E)∧(┓F→(D→┓E 2020-06-17 …
氢化钙固体是登山运动员常用的能源提供剂。某兴趣小组拟选用如下装置制备氢化钙,仪器连接顺序正确的是( 2020-06-21 …
设一数列a,b,c,d,e,f,通过栈结构不可能不可能排成的顺序数列为()A)c,b,e,f,d, 2020-06-28 …
如图,灰太狼从A出发,不断往返于AB之间,懒羊羊从C出发按C-E-F-D围绕矩形不断行走.已知AC 2020-07-05 …
如图,甲从A出发,不断往返于A、B两地,乙从C出发,沿C-E-F-D-C围绕矩形不断行走,两人同时出 2020-10-30 …
如图,甲从A出发,不断往返于AB之间行走.乙从C出发,沿C-E-F-D-C围绕矩形不断行走.甲的速度 2020-11-08 …