早教吧作业答案频道 -->数学-->
在平面直角坐标系中,抛物线y=x2-6mx+5与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).(1)当b=1时,求抛物线相应的函数表达式;(2)当b=1时,如图,E(t,0)是线段BC上
题目详情
在平面直角坐标系中,抛物线y=x2-6mx+5与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).
(1)当b=1时,求抛物线相应的函数表达式;
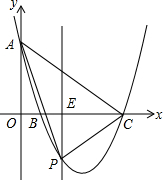
(2)当b=1时,如图,E(t,0)是线段BC上的一动点,过点E作平行于y轴的直线l与抛物线的交点为P.求△APC面积的最大值;
(3)当c=b+n时,且n为正整数,线段BC(包括端点)上有且只有五个点的横坐标是整数,求b的值.

(1)当b=1时,求抛物线相应的函数表达式;
(2)当b=1时,如图,E(t,0)是线段BC上的一动点,过点E作平行于y轴的直线l与抛物线的交点为P.求△APC面积的最大值;
(3)当c=b+n时,且n为正整数,线段BC(包括端点)上有且只有五个点的横坐标是整数,求b的值.
▼优质解答
答案和解析
(1)当b=1时,将点B(1,0)代入抛物线y=x2-6mx+5中,得m=1,
∴y=x2-6x+5;
(2)如图1中,直线AC与PE交于点F.
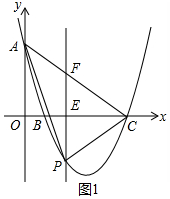
当b=1时,求得A(0,5),B(1,0),C(5,0),可得AC所在的一次函数表达式为y=-x+5,
∵E(t,0),
∴P (t,t2-6t+5),直线l与AC的交点为F(t,-t+5),
∴PF=(-t+5)-(t2-6t+5)=-t2+5t,
∴S△APC=
×(-t2+5t)•5=-
(t-
)2+
,
∵-
<0,
∴当t=
时,面积S有最大值
;
(3)①当b整数时,n为整数,
∴n=4,c=b+4.则b,b+4是方程x2-mx+5=0的两个根,分别代入方程中,
得b2-mb+5=0 ①,(b+4)2-m(b+4)+5=0 ②,
由①②可得b2+4b-5=0,解得b=1或-5(舍);
或由一元二次方程根与系数的关系得 b(b+4)=5解得b=1或-5(舍).
②当b小数时,n为整数,∴n=5,c=b+5为小数,则b,b+5是方程x2-mx+5=0的两个根,同样可得b=
或
(舍弃);
∴b=1或
.
∴y=x2-6x+5;
(2)如图1中,直线AC与PE交于点F.

当b=1时,求得A(0,5),B(1,0),C(5,0),可得AC所在的一次函数表达式为y=-x+5,
∵E(t,0),
∴P (t,t2-6t+5),直线l与AC的交点为F(t,-t+5),
∴PF=(-t+5)-(t2-6t+5)=-t2+5t,
∴S△APC=
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 125 |
| 8 |
∵-
| 5 |
| 2 |
∴当t=
| 5 |
| 2 |
| 125 |
| 8 |
(3)①当b整数时,n为整数,
∴n=4,c=b+4.则b,b+4是方程x2-mx+5=0的两个根,分别代入方程中,
得b2-mb+5=0 ①,(b+4)2-m(b+4)+5=0 ②,
由①②可得b2+4b-5=0,解得b=1或-5(舍);
或由一元二次方程根与系数的关系得 b(b+4)=5解得b=1或-5(舍).
②当b小数时,n为整数,∴n=5,c=b+5为小数,则b,b+5是方程x2-mx+5=0的两个根,同样可得b=
-5+3
| ||
| 2 |
-5-3
| ||
| 2 |
∴b=1或
-5+3
| ||
| 2 |
看了 在平面直角坐标系中,抛物线y...的网友还看了以下:
1.已知f(x),g(x)均为R上的奇函数且f(x)>0解集为(4,10),g(x)>0解集为(2 2020-05-14 …
有大于零的极值点是什么意思“由于函数y=eˆx+ax,x∈R有大于零的极值点,故y'=e^x+a有 2020-05-23 …
当X→0时,limsinx/x=1成立,而limxsin1/x可以化为lim(sin1/x÷1/x 2020-06-02 …
求数学分段函数f(x)={xsin1/x(x不等于0)0(x=0)}为什么在-1,1上满足不了罗尔 2020-06-19 …
请教一道大学物理题.简谐运动的.一质点沿x轴以x=0为平衡位置作简谐运动,频率为0.25hz,t= 2020-06-29 …
1.我想问一个很基础的问题.1/x=1,当x=0时,左边无意义,那么无意义=1成立吗,x=0为什么不 2020-10-31 …
已知x^2-5x+1=0求x^2+1/x^2语言描述:x的平方减5x加1等于0求x的平方加x平方分之 2020-10-31 …
x^2=0为什么有两个根的问题,上式是x平方等于0的式子,这是中学的数学,书上说他有两个根x1=x2 2020-10-31 …
设函数f(x)={2/x^2+1,x≤0;ax+b,x>0}为使函数f(x)在x=1处连续且可导,a 2020-11-03 …
反常积分瑕点选取的问题∫(0,1)dx/√x(1-x^2)为什么不用考虑x=1为瑕点,而考虑x=0为 2021-01-02 …