早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.(1)求证:AD平分∠BAC;(2)若CD=1,求图中阴影部分的面积(结果保留π).
题目详情
如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
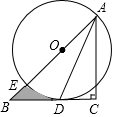
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).

(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
▼优质解答
答案和解析
(1)证明:连接DE,OD.
∵BC相切⊙O于点D,
∴∠CDA=∠AED,
∵AE为直径,
∴∠ADE=90°,
∵AC⊥BC,
∴∠ACD=90°,
∴∠DAO=∠CAD,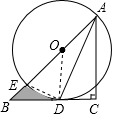
∴AD平分∠BAC;
(2)∵在Rt△ABC中,∠C=90°,AC=BC,
∴∠B=∠BAC=45°,
∵BC相切⊙O于点D,
∴∠ODB=90°,
∴OD=BD,∴∠BOD=45°,
设BD=x,则OD=OA=x,OB=
x,
∴BC=AC=x+1,
∵AC2+BC2=AB2,
∴2(x+1)2=(
x+x)2,
∴x=
,
∴BD=OD=
,
∴图中阴影部分的面积=S△BOD-S扇形DOE=
×
×
-
=1-
.
∵BC相切⊙O于点D,
∴∠CDA=∠AED,
∵AE为直径,
∴∠ADE=90°,
∵AC⊥BC,
∴∠ACD=90°,
∴∠DAO=∠CAD,

∴AD平分∠BAC;
(2)∵在Rt△ABC中,∠C=90°,AC=BC,
∴∠B=∠BAC=45°,
∵BC相切⊙O于点D,
∴∠ODB=90°,
∴OD=BD,∴∠BOD=45°,
设BD=x,则OD=OA=x,OB=
| 2 |
∴BC=AC=x+1,
∵AC2+BC2=AB2,
∴2(x+1)2=(
| 2 |
∴x=
| 2 |
∴BD=OD=
| 2 |
∴图中阴影部分的面积=S△BOD-S扇形DOE=
| 1 |
| 2 |
| 2 |
| 2 |
45•π×(
| ||
| 360 |
| π |
| 4 |
看了 如图,在Rt△ABC中,∠C...的网友还看了以下:
(2007·临沂模拟)下图中的图A为某生物体细胞有丝分裂示意图,图B表示在一个细胞周期(G1,S, 2020-04-05 …
(图:)\x0d\x0d下图中的图A为某生物体细胞有丝分裂示意图,图B表示在一个细胞周期(G1、、 2020-04-06 …
下图中的图A为某生物体细胞有丝分裂示意图,图B表示在一个细胞周期(G1、、S、G2组成分裂间期,M 2020-04-06 …
下图中的图A为某生物体细胞有丝分裂示意图,图B表示在一个细胞周期(G.、S、@组成若图A所示细胞来 2020-04-06 …
下列比较大小中,正确的是A–(–9)<–(+9)B–3/4<–1/4C–|–下列比较大小中,正确的 2020-05-14 …
在我国,保险公司每一会计年度向分红保单持有人实际分配盈余的比例不低于当年可分配盈余的( )。A.9 2020-05-22 …
一块最小分度值为0.2 MPa的普通弹簧管式压力表,在检定时出现以下数据,只有()可能是正确的。A. 2020-06-07 …
小燕在少年宫猜谜室里发现一个有趣的图形,9盏绿灯纵横交错的排成十行.而且每行都是三盏灯,请画出它的 2020-06-25 …
下列式子中a和b(a,b都不为0)成反比例的是()A.9*a=2*bB.a*(2/3)-4/b=0 2020-07-09 …
根据图中的图A和图B,回答问题(1)图A表示动作,图B表示动作.(2)人在屈肘时,图A、中的两种肌 2020-07-16 …