早教吧作业答案频道 -->数学-->
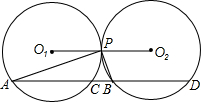
如图,O1和O2是外切于点P的两个等圆,点A、B分别在O1、O2上,∠APB=90°,和O1、O2的另一个交点分别是C、D.求证:CD=O1O2.
题目详情
如图, O1和 O2是外切于点P的两个等圆,点A、B分别在 O1、 O2上,∠APB=90°,和 O1、 O2的另一个交点分别是C、D.求证:CD=O1O2.

▼优质解答
答案和解析
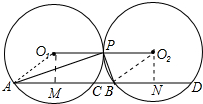
证明:连接O1O2,AO1,BO2,作O1M⊥AD于M,O2N⊥AD于N.
 ∵ O1和 O2外切于点P,
∵ O1和 O2外切于点P,
∴接O1O2经过点P,
∵PA⊥PB,
∴∠APB=90°,
∴∠PAB+∠PBA=90°,∠APO1+∠BPO2=90°,
∵O1A=O1P,O2P=O2B,
∴∠O1AP=∠O1PA,∠O2PB=∠O2BP,
∴∠O1AB+∠O2BA=∠O1AP+∠PAB+∠PBA+∠O2BP=180°,
∴AO1∥BO2,∵AO1=BO2,
∴四边形ABO2O1是平行四边形,
∴AB=O1O2=2r.O1O2∥AB,
∵O1M∥O2N,
∴四边形MNO2O1是平行四边形,
∴O1M=O2N,∵O1M⊥AD,O2N⊥AD,
∴AC=BD(弦心距相等弦相等),
∴AB=CD,
∴CD=2r.
 ∵ O1和 O2外切于点P,
∵ O1和 O2外切于点P,∴接O1O2经过点P,
∵PA⊥PB,
∴∠APB=90°,
∴∠PAB+∠PBA=90°,∠APO1+∠BPO2=90°,
∵O1A=O1P,O2P=O2B,
∴∠O1AP=∠O1PA,∠O2PB=∠O2BP,
∴∠O1AB+∠O2BA=∠O1AP+∠PAB+∠PBA+∠O2BP=180°,
∴AO1∥BO2,∵AO1=BO2,
∴四边形ABO2O1是平行四边形,
∴AB=O1O2=2r.O1O2∥AB,
∵O1M∥O2N,
∴四边形MNO2O1是平行四边形,
∴O1M=O2N,∵O1M⊥AD,O2N⊥AD,
∴AC=BD(弦心距相等弦相等),
∴AB=CD,
∴CD=2r.
看了 如图,O1和O2是外切于点P...的网友还看了以下:
不用《搜查证》也可以进行搜查的情形是() A.其他见证人在场的B.有他的家属在场的C.有邻居在场的 2020-05-18 …
不用搜查证也可以进行搜查的情形是( )。A.其他见证人在场的B.有他的家属在场的C.有邻居在场的D. 2020-05-19 …
导游人员有( )等情形的,应受到吊销导游证的处罚。A、进行导游活动时未佩带导游证的B、私自承担导 2020-05-19 …
导游人员有( )等情形的,应受到吊销导游证的处罚。 A.进行导游活动时未佩带导游证的B 2020-05-20 …
可以全额发放留学贷款的信用担保是( )。A.有第三方提供信用担保,但不提供连带责任保证的B.银行认 2020-05-22 …
有下列情形之一的,保证人不承担民事责任()A.主合同当事人双方串通,骗取保证人提供保证的B.主 2020-05-27 …
下列阐述正确的是()A.牛顿第一定律是能够直接通过实验验证的B.足球离开运动员的脚后,仍然向前滚动 2020-06-16 …
下列说法正确的是()A.在探究太阳对行星的引力规律时,我们引用了公式F=mv2r,这个关系式实际上是 2020-11-11 …
在下列论断中,揭示了“马克思主义哲学既是科学的世界观,又是科学的方法论”的选项是A.马克思主义哲学对 2020-11-14 …
下列说法有误的一项()A.由于古代的官员的人数占人口总数比例较小,所以古代大部分人是没有身份证的B. 2020-12-10 …