某工地一传输工件的装置可简化为如图所示的情形，AB为一段足够大的14圆弧固定轨道，圆弧半径R=5.6m，BC为一段足够长的水平轨道，CD为一段14圆弧固定轨道，圆弧半径r=1m，三段轨道均光滑

Question

某工地一传输工件的装置可简化为如图所示的情形，AB为一段足够大的(1)/(4)圆弧固定轨道，圆弧半径R=5.6m，BC为一段足够长的水平轨道，CD为一段(1)/(4)圆弧固定轨道，圆弧半径r=1m，三段轨道均光滑．一长为L=2m、质量为M=1kg的平板小车最初停在BC轨道的最左端，小车上表面刚好与AB轨道相切，且与CD轨道最低点处于同一水平面．一可视为质点、质量为m=2kg的工件从距AB轨道最低点h高处沿轨道自由滑下，滑上小车后带动小车也向右运动，小车与CD轨道左端碰撞（碰撞时间极短）后即被粘在C处．工件只有从CD轨道最高点飞出，才能被站在台面DE上的工人接住．工件与小车的动摩擦因数为μ=0.5，取g=10m/s²，求：

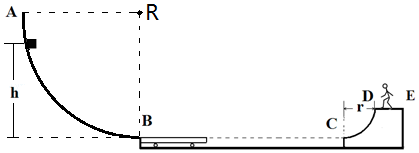
（1）若h为2.8m，则工件滑到圆弧底端B点时对轨道的压力为多大？
（2）要使工件能被站在台面DE上的工人接住h的取值范围．

Answer 1

（1）工件从起点滑到圆弧轨道底端B点，设到B点时的速度为V_B，根据动能定理：
  mgh=(1)/(2)m

v

2 B

…①
工件做圆周运动，在B点，由牛顿第二定律得：
  N-mg=m(v2B)/(R)…②
由①②两式可解得：N=40N     
由牛顿第三定律知，工件滑到圆弧底端B点时对轨道的压力为 N′=N=40N     
（2）①由于BC轨道足够长，要使工件能到达CD轨道，工件与小车必须能达共速，设工件刚滑上小车时的速度为v₀，工件与小车达共速时的速度为v₁，假设工件到达小车最右端才与其共速，规定向右为正方向，则对于工件与小车组成的系统，由动量守恒定律得：
  mv₀=（m+M）v₁ ③
由能量守恒定律得：μmgL=(1)/(2)m

v

2 0

-(1)/(2)(m+M)

v

2 1

       ④
对于工件从AB轨道滑下的过程，由机械能守恒定律得：
   mgh₁=(1)/(2)m

v

2 0

          ⑤
代入数据解得：h₁=3m．                        
②要使工件能从CD轨道最高点飞出，h₁=3m为其从AB轨道滑下的最大高度，设其最小高度为h′，刚滑上小车的速度为v₀′，与小车达共速时的速度为v₁′，刚滑上CD轨道的速度为v₂′，规定向右为正方向，由动量守恒定律得：
mv₀′=（m+M）v₁′…⑥
由能量守恒定律得：
   μmgL=(1)/(2)m

v

′2 0

-(1)/(2)M

v

′2 1

-(1)/(2)m

v

′2 2

   ⑦
工件恰好滑到CD轨道最高点，由机械能守恒定律得：
   (1)/(2)m

v

′2 2

=mgr     ⑧
工件在AB轨道滑动的过程，由机械能守恒定律得：
   mgh′=(1)/(2)m

v

′2 0

           ⑨
联立．⑥⑦⑧⑨，代入数据解得：h′=(18)/(7)m     
综上所述，要使工件能到达CD轨道最高点，应使h满足：(18)/(7)m<h≤3m．
答：（1）若h为2.8m，则工件滑到圆弧底端B点时对轨道的压力为40N．
（2）要使工件能被站在台面DE上的工人接住h的取值范围是(18)/(7)m<h≤3m．