早教吧作业答案频道 -->数学-->
如图,在四棱锥P-ABCD中,底面ABCD是菱形,AC∩BD=O.(1)若AC⊥PD,求证:AC⊥平面PBD;(2)若平面PAC⊥平面ABCD,求证:|PB|=|PD|.
题目详情
如图,在四棱锥P-ABCD中,底面ABCD是菱形,AC∩BD=O.
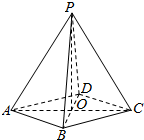
(1)若AC⊥PD,求证:AC⊥平面PBD;
(2)若平面PAC⊥平面ABCD,求证:|PB|=|PD|.

(1)若AC⊥PD,求证:AC⊥平面PBD;
(2)若平面PAC⊥平面ABCD,求证:|PB|=|PD|.
▼优质解答
答案和解析
证明:(1)因为底面ABCD是菱形,所以AC⊥BD.
又因为AC⊥PD,PD∩BD=D,
所以AC⊥平面PBD…(4分)
(2)由(1)知AC⊥BD.
因为平面PAC⊥平面ABCD,平面PAC∩平面ABCD=AC,
BD⊂平面ABCD,
所以BD⊥平面PAC.
因为PO⊂平面PAC,
所以BD⊥PO.
因为底面ABCD是菱形,
所以|BO|=|DO|,
所以|PB|=|PD|.…(10分)
又因为AC⊥PD,PD∩BD=D,
所以AC⊥平面PBD…(4分)

(2)由(1)知AC⊥BD.
因为平面PAC⊥平面ABCD,平面PAC∩平面ABCD=AC,
BD⊂平面ABCD,
所以BD⊥平面PAC.
因为PO⊂平面PAC,
所以BD⊥PO.
因为底面ABCD是菱形,
所以|BO|=|DO|,
所以|PB|=|PD|.…(10分)
看了 如图,在四棱锥P-ABCD中...的网友还看了以下:
菱形ABCD的两条对角线相交于点O,AC=4.2,BD=3,分别在线段OA,OB.OC.OD,上取 2020-05-17 …
《菱子到处都是》这则寓言说明了什么?原文:北方有一个人,从来没见过菱。他去南方做官,在接风筵席上吃 2020-06-23 …
1.现有一菱形草坪,横穿草坪的两条小路AC、BD,分别为60m,80m;为防游人踏入草坪,需在菱形 2020-06-28 …
求光栅常数d一束具有两种波长a和d的平行光垂直照射到一衍射光栅上,测得波长a的第三极主极大衍射角和 2020-07-10 …
命题“菱形的四条边相等”的否命题是A.四条边相等的四边形是菱形B.四条边不相等的四边形不是菱形C. 2020-07-15 …
请教一下数据库里的关系题1、在关系模式R(A,B,C,D)中,有函数依赖集F={B→C,C→D,D→ 2020-11-03 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …
面积是2500的矩形、三角形、菱形各有几个?边长是整数,面积是2500的矩形、三角形、菱形各有几个? 2020-12-25 …
“我们可以得到A和B分别与C、D、E之间的关系”这句话用英语怎么表达“我们可以得到A和B分别与C、D 2020-12-25 …
关于c赋值#includemain(){\x05intb=3;\x05intarr[]={6,7,8 2020-12-31 …