早教吧作业答案频道 -->数学-->
图中是小明设计的带正方形图案的花边作品,该作品由形如图乙的矩形图案及轴对称图形拼接而成(不重叠,无缝隙),图乙中,点E,F分别是矩形ABCD的边AD、BC的中点,两条平行线AL,CK分
题目详情
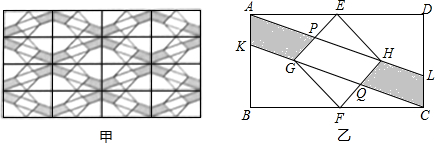
图中是小明设计的带正方形图案的花边作品,该作品由形如图乙的矩形图案及轴对称图形拼接而成(不重叠,无缝隙),图乙中,点E,F分别是矩形ABCD的边AD、BC的中点,两条平行线AL,CK分别经过正方形顶点H,G和正方形的边EG,FH的中点P,Q,测得PG=2cm,则图乙中两个阴影四边形的面积之和为___cm2.

▼优质解答
答案和解析
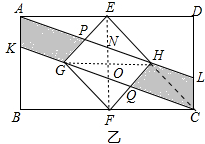
如图,连接HC、EF、GH,EF分别与GH、AL交于O、N.
∵四边形ABCD是矩形,AE=ED,BF=FC,
∴AE∥BF,AE=BF,
∴四边形ABFE是平行四边形,∵∠B=90°,
∴四边形AEFB是矩形,同理四边形EFCD是矩形,
∵四边形EGFH是正方形,
∴GH⊥EF,
∴∠GOF=∠AEF=90°,
∴GH∥AE,
∴
=
=1,
∴AE=ED=GH=EF,
∴四边形ABFE,四边形EFCD是正方形,
∴∠FEH=∠EFH=∠HED=45°,
∴E、H、C共线,点H是正方形EDCF的对角线的交点,
∵EN∥CL,EH=CH,
∴
=
=
=1,
∴HN=HL,EN=CL,
∴△EHN≌△CHL,
∴S△CHL=S△ENH,
∵HO∥AE,
∴
=
=
,
∴OE=
EN,
∴S△ENH=
S△EOH,
根据对称性可知,AC=CQ=PH=GQ,FQ=QH,
∴S△QCH=S△GQH=
S△GHF,
∵PG=PE=2,
∴EG=EH=4,
∴S△EOH=
×42=4,S△GHF=
×42=8,
∴S△CHL+S△CHQ=
×4+4=
,
∴S阴=2×
=
.
故答案为
.

∵四边形ABCD是矩形,AE=ED,BF=FC,
∴AE∥BF,AE=BF,
∴四边形ABFE是平行四边形,∵∠B=90°,
∴四边形AEFB是矩形,同理四边形EFCD是矩形,
∵四边形EGFH是正方形,
∴GH⊥EF,
∴∠GOF=∠AEF=90°,
∴GH∥AE,
∴
| AE |
| GH |
| PE |
| PG |
∴AE=ED=GH=EF,
∴四边形ABFE,四边形EFCD是正方形,
∴∠FEH=∠EFH=∠HED=45°,
∴E、H、C共线,点H是正方形EDCF的对角线的交点,
∵EN∥CL,EH=CH,
∴
| HN |
| HL |
| EH |
| HC |
| EN |
| CL |
∴HN=HL,EN=CL,
∴△EHN≌△CHL,
∴S△CHL=S△ENH,
∵HO∥AE,
∴
| OH |
| AE |
| ON |
| NE |
| 1 |
| 2 |
∴OE=
| 3 |
| 2 |
∴S△ENH=
| 2 |
| 3 |
根据对称性可知,AC=CQ=PH=GQ,FQ=QH,
∴S△QCH=S△GQH=
| 1 |
| 2 |
∵PG=PE=2,
∴EG=EH=4,
∴S△EOH=
| 1 |
| 4 |
| 1 |
| 2 |
∴S△CHL+S△CHQ=
| 2 |
| 3 |
| 20 |
| 3 |
∴S阴=2×
| 20 |
| 3 |
| 40 |
| 3 |
故答案为
| 40 |
| 3 |
看了 图中是小明设计的带正方形图案...的网友还看了以下:
用几何图形(圆形 长方形 正方形 三角形)拼图,可以拼成什么图形?急需,谢谢!用几何图形(圆形 长 2020-05-16 …
(1)一幅图案,在某个顶点处由三个边长相等的正多边形镶嵌而成,其中的两个分别是正方形和正六边形,则 2020-05-17 …
分解因式:3mp^2+12mpq+12mq^2还有一题:现有如图正方形①1个,正方形②3个和长方形 2020-05-17 …
附加题(1)一幅图案,在某个顶点处由三个边长相等的正多边形镶嵌而成.其中的两个分别是正方形和正六边 2020-05-17 …
考考你,摆火材棍用火柴棍拼图形,只能用端点连接,不能交叉,不能折断拼一个正方形至少需要4根,那拼5 2020-05-17 …
如图所示,用大小相等的小正方形拼大正方形,拼第一个正方形需要4个小正方形,拼第二个正方形需要9个小 2020-05-17 …
制作,拼图题.(1)制作要求:用一个边长为4cm的正方形纸板制作的七巧板.(2)拼图要求:先将七巧 2020-05-17 …
用三个单位正方形,仅能拼出和两种不同图形(拼图时要求两个相接的单位正方形有一条边完全重合,并且各正 2020-05-17 …
如图:点P是边长为1的正方形内(不在边上)任意一点,P和正方形各顶点相连后把正方形分成4块,其中① 2020-07-24 …
图1、图2、图3均是单位为1的方格图.(1)请把方格图1中的带阴影的图形适当剪开,重新拼成正方形;( 2021-01-15 …