早教吧作业答案频道 -->数学-->
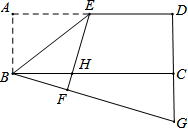
已知如图,在矩形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则FH=.
题目详情
已知如图,在矩形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则FH=___.

▼优质解答
答案和解析
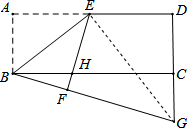 连结GE.
连结GE.
∵E是边AD的中点,
∴DE=AE=FE,
又∵四边形ABCD是矩形,
∴∠D=∠A=∠BFE=90°,
∴∠D=∠EFG=90°.
在Rt△EFG与Rt△EDG中,
,
∴Rt△EFG≌Rt△EDG(HL);
∴DG=FG=16,
设DC=x,则CG=16-x,BG=x+16
在Rt△BCG中,
BG2=BC2+CG2,
即(x+16)2=(16-x)2+242,
解得x=9,
∵AD∥BC,
∴∠AEB=∠CBE,
∵∠AEB=∠FEB,
∴∠CBE=∠FEB,
∴BH=EH,
设BH=EH=y,则FH=12-y,
在Rt△BFH中,
BH2=BF2+FH2,
即y2=92+(12-y)2,
解得y=
,
∴12-y=12-
=
.
故答案为:
.
 连结GE.
连结GE.∵E是边AD的中点,
∴DE=AE=FE,
又∵四边形ABCD是矩形,
∴∠D=∠A=∠BFE=90°,
∴∠D=∠EFG=90°.
在Rt△EFG与Rt△EDG中,
|
∴Rt△EFG≌Rt△EDG(HL);
∴DG=FG=16,
设DC=x,则CG=16-x,BG=x+16
在Rt△BCG中,
BG2=BC2+CG2,
即(x+16)2=(16-x)2+242,
解得x=9,
∵AD∥BC,
∴∠AEB=∠CBE,
∵∠AEB=∠FEB,
∴∠CBE=∠FEB,
∴BH=EH,
设BH=EH=y,则FH=12-y,
在Rt△BFH中,
BH2=BF2+FH2,
即y2=92+(12-y)2,
解得y=
| 75 |
| 8 |
∴12-y=12-
| 75 |
| 8 |
| 21 |
| 8 |
故答案为:
| 21 |
| 8 |
看了 已知如图,在矩形ABCD中,...的网友还看了以下:
1、它是一个奇数,也是一个合数,它是3的倍数,也是18的因数,这个数是()A:3.B:6.C:9. 2020-06-07 …
(1/2)已知直线l:y=x+b及圆C:x^2+y^2=1,存在b,使自A(3,3)发出的光线被直 2020-06-09 …
如图1,AB是O的直径,E是AB延长线上一点,EC切O于点C,OP⊥AO交AC于点P,交EC的延长 2020-06-13 …
如图,AB是⊙O的直径,DF切⊙O于点D,BF⊥DF于F,过点A作AC∥BF交BD的延长线于点C. 2020-06-15 …
公元前547年,季札被封于延陵,史称“延陵季子”.“延陵”从此成为常州在历史上第一个见于史籍的名称 2020-07-11 …
几何的比例线段(只是填空)1.如果线段a=3cm,b=1.5cm,那么a与b的比值是.2.a是2、 2020-07-25 …
(2012•许昌二模)如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB 2020-08-01 …
如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB与O1O2的延长线相交 2020-08-01 …
已知:如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,在射线PA上截取PD=PC, 2020-11-03 …
如图点0在角APB的角平分线上圆0与PA相切于点C求证直线PB与圆O相切,PO的延长线与圆0交于点E 2021-01-11 …