早教吧作业答案频道 -->数学-->
如图,在四棱锥P-ABCD中,△ACD是正三角形,BD垂直平分AC,垂足为M,∠ABC=120°,PA=AB=1,PD=2,N为PD的中点.(1)求证:AD⊥平面PAB;(2)求证:CN∥平面PAB.
题目详情
如图,在四棱锥P-ABCD中,△ACD是正三角形,BD垂直平分AC,垂足为M,∠ABC=120°,PA=AB=1,PD=2,N为PD的中点.
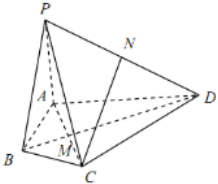
(1)求证:AD⊥平面PAB;
(2)求证:CN∥平面PAB.

(1)求证:AD⊥平面PAB;
(2)求证:CN∥平面PAB.
▼优质解答
答案和解析
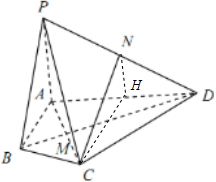 证明:(1)∵BD是AC的中垂线,∠ABC=120°,
证明:(1)∵BD是AC的中垂线,∠ABC=120°,
∴∠ABM=60°,∠AMB=90°,∵AB=1,∴AM=
.∠BAM=30°.
∵△ACD是正三角形,∴AD=2AM=
,∠DAC=60°,
∴∠BAD=∠BAM+∠DAC=90°,∴AB⊥AD.
又PA=1,PD=2,∴PA2+AD2=PD2,即PA⊥AD.
又PA⊂平面PAB,AB⊂平面PAB,PA∩AB=A,
∴AD⊥平面PAB.
(2)取AD的中点H,连结NH,CH.
∵△ACD是正三角形,∴CH⊥AD,
∵N,H是PD,AD的中点,∴NH∥PA,
∵PA⊥AD,∴NH⊥AD.
又NH⊂平面NCH,CH⊂平面NCH,NH∩CH=H,
∴AD⊥平面NCH,又AD⊥平面PAB,
∴平面NCH∥平面PAB.
∵CN⊂平面NCH,
∴CN∥平面PAB.
 证明:(1)∵BD是AC的中垂线,∠ABC=120°,
证明:(1)∵BD是AC的中垂线,∠ABC=120°,∴∠ABM=60°,∠AMB=90°,∵AB=1,∴AM=
| ||
| 2 |
∵△ACD是正三角形,∴AD=2AM=
| 3 |
∴∠BAD=∠BAM+∠DAC=90°,∴AB⊥AD.
又PA=1,PD=2,∴PA2+AD2=PD2,即PA⊥AD.
又PA⊂平面PAB,AB⊂平面PAB,PA∩AB=A,
∴AD⊥平面PAB.
(2)取AD的中点H,连结NH,CH.
∵△ACD是正三角形,∴CH⊥AD,
∵N,H是PD,AD的中点,∴NH∥PA,
∵PA⊥AD,∴NH⊥AD.
又NH⊂平面NCH,CH⊂平面NCH,NH∩CH=H,
∴AD⊥平面NCH,又AD⊥平面PAB,
∴平面NCH∥平面PAB.
∵CN⊂平面NCH,
∴CN∥平面PAB.
看了 如图,在四棱锥P-ABCD中...的网友还看了以下:
某次数学考试,平平.元元.方方.婷婷.卉卉5人的成绩统计是:平平.元元.方方.婷婷的平均分是75分, 2020-03-30 …
五位老师给吴欣作文评分,去掉一个最高分,平均分86;去掉一个最低分,平均得分90分,如果去掉一个最 2020-04-07 …
如下表,a,b,c,d,e,f均为有理数.表中各行各列、两对角线上三个数之和都相等,试计算(d分之 2020-05-23 …
有五个足球队A、B、C、D、E分入同一小组进行单循环足球比赛,争夺出线权,比赛规定:胜一场得3分, 2020-06-11 …
若a,b,c,d,都是质数,切a的平方+b的平方+c的平方+d的平方=78,a的平方-b的平方=c 2020-07-09 …
如图,∠EAF=90°,B、D分别在射线AE和AF上,且AB=AD,过B和D分别作AE和AF的垂线 2020-07-20 …
已知b分之a=d分之c,求证:点开看,打不下了-求证a平方分之一+b平方分之一+c平方分之一+d平 2020-07-25 …
如图,在四棱锥D′-ABCE中,底面为直角梯形,AB=2BC=2CE=2,且AB⊥BC,AB∥CE 2020-07-31 …
A.B.C.D.E五个队分在同一小组进行单循环足球比赛,争夺出现权,比赛规则规定:胜一场得3分,平一 2020-12-06 …
把符合要求的图形序号填在括号里.A、正方形B、长方形C、平行四边形D、梯形(1)两组对边分别平行,有 2021-02-05 …