如图，已知椭圆C的中心为原点O，F（-25，0）为C的左焦点，P为C上一点，满足|OP|=|OF|且|PF|=4，则椭圆C的方程为（）A.x225+y25=1B.x230+y210=1C.x236+y216=1D.x245+y225=1

Question

如图，已知椭圆C的中心为原点O，F（-2

√(5)，0）为C的左焦点，P为C上一点，满足|OP|=|OF|且|PF|=4，则椭圆C的方程为（　　）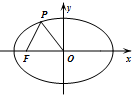

A.

(x2)/(25)+(y2)/(5)=1

B.

(x2)/(30)+(y2)/(10)=1

C.

(x2)/(36)+(y2)/(16)=1

D.

(x2)/(45)+(y2)/(25)=1

Answer 1

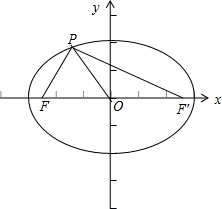由题意可得c=2√(5)，设右焦点为F′，由|OP|=|OF|=|OF′|知，∠PFF′=∠FPO，∠OF′P=∠OPF′，
所以∠PFF′+∠OF′P=∠FPO+∠OPF′，
由∠PFF′+∠OF′P+∠FPO+∠OPF′=180°知，∠FPO+∠OPF′=90°，即PF⊥PF′．
在Rt△PFF′中，由勾股定理，得|PF′|=√(FF′2-PF2)=√((4√(5))2-42)=8，
由椭圆定义，得|PF|+|PF′|=2a=4+8=12，从而a=6，得a²=36，
于是 b²=a²-c²=36-(2√(5))2=16，
所以椭圆的方程为(x2)/(36)+(y2)/(16)=1．
故选：C．