早教吧作业答案频道 -->数学-->
阿基米德折弦定理:如图1,AB和BC是O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是ABC的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.下
题目详情
阿基米德折弦定理:如图1,AB和BC是 O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是
的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.
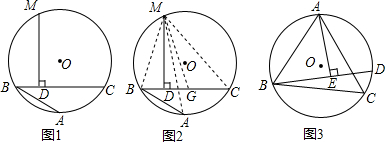
下面是运用“截长法”证明CD=AB+BD的部分证明过程.
证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是
的中点,
∴MA=MC
任务:(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图(3),已知等边△ABC内接于 O,AB=2,D为
上 一点,∠ABD=45°,AE⊥BD于点E,则△BDC的周长是___.
 |
| ABC |

下面是运用“截长法”证明CD=AB+BD的部分证明过程.
证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是
 |
| ABC |
∴MA=MC
任务:(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图(3),已知等边△ABC内接于 O,AB=2,D为
 |
| AC |
▼优质解答
答案和解析
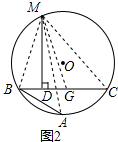 (1)证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.
(1)证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是
的中点,
∴MA=MC.
在△MBA和△MGC中
,
∴△MBA≌△MGC(SAS),
∴MB=MG,
又∵MD⊥BC,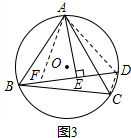
∴BD=GD,
∴DC=GC+GD=AB+BD;
(2) 如图3,截取BF=CD,连接AF,AD,CD,
由题意可得:AB=AC,∠ABF=∠ACD,
在△ABF和△ACD中
∵
,
∴△ABF≌ACD(SAS),
∴AF=AD,
∵AE⊥BD,
∴FE=DE,则CD+DE=BE,
∵∠ABD=45°,
∴BE=
=
,
则△BDC的周长是2+2
.
故答案为:2+2
.
 (1)证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.
(1)证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG.∵M是
 |
| ABC |
∴MA=MC.
在△MBA和△MGC中
|
∴△MBA≌△MGC(SAS),
∴MB=MG,
又∵MD⊥BC,

∴BD=GD,
∴DC=GC+GD=AB+BD;
(2) 如图3,截取BF=CD,连接AF,AD,CD,
由题意可得:AB=AC,∠ABF=∠ACD,
在△ABF和△ACD中
∵
|
∴△ABF≌ACD(SAS),
∴AF=AD,
∵AE⊥BD,
∴FE=DE,则CD+DE=BE,
∵∠ABD=45°,
∴BE=
| AB | ||
|
| 2 |
则△BDC的周长是2+2
| 2 |
故答案为:2+2
| 2 |
看了 阿基米德折弦定理:如图1,A...的网友还看了以下:
下列叙述中不正确的一条是.A.一个正数的相反数是负数,一个负数的相反数是正数B.在数轴上与原点距离相 2020-03-30 …
不能使两个直角三角形全等的条件A一条直角边及其对角对应相等B斜边和一条直角边对应相等C斜边和一锐角 2020-04-11 …
要获得物体的投影必须具备( )个条件.A.一B.二C.三D.四 2020-05-31 …
下列哪项不是种子正常萌发的外界条件A.一定的水分B.充足的空气C.胚完整且是活的D.适宜的温度 2020-06-27 …
分别将下列条件中的哪两个条件组合,可以判定四边形ABCD是平行四边形?1.AB//CD2.BC// 2020-07-21 …
如图直线a,b相交构成四个角为∠1在图中添加一条直线c,与直线a,b都相交在所得的角中标出∠2,∠ 2020-07-23 …
一个平角有()条边.A.一B.两C.三 2020-07-30 …
一个三角形最多可以画()条高.A.一B.二C.三D.四 2020-11-03 …
一道关于ASCⅡ码的选择题下列叙述中,正确的一条是().A)一个字符的标准ASCⅡ码占一个字节的存储 2020-11-07 …
如图,下列选项中不遵循基因自由组合定律的是()AD在一条染色体上,ad在另一条染色体上这两条互为同源 2020-12-28 …