早教吧作业答案频道 -->数学-->
我们知道,求圆环的面积可以转化为求大圆与小圆面积的差.(1)如图①,直线l与小圆相切于点P,与大圆相交于点A,B.①求证:AP=BP;②若AB=10,求圆环的面积;(2)如图②,直线l与大
题目详情
我们知道,求圆环的面积可以转化为求大圆与小圆面积的差.
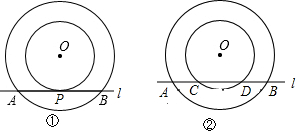
(1)如图①,直线l与小圆相切于点P,与大圆相交于点A,B.
①求证:AP=BP;
②若AB=10,求圆环的面积;
(2)如图②,直线l与大圆、小圆分别交于点A,B,C,D,若AB=10,AC=2,则圆环的面积为___.

(1)如图①,直线l与小圆相切于点P,与大圆相交于点A,B.
①求证:AP=BP;
②若AB=10,求圆环的面积;
(2)如图②,直线l与大圆、小圆分别交于点A,B,C,D,若AB=10,AC=2,则圆环的面积为___.
▼优质解答
答案和解析
(1)①证明:连结OP,如图①,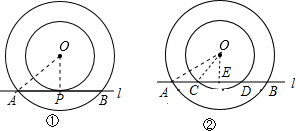
∵直线l与小圆相切于点P,
∴OP⊥AB,
∴AP=BP;
② 连结OA,如图①,AP=BP=
AB=5,
在Rt△OPA中,OA2-OP2=AP2=25,
∴圆环的面积=S大圆-S小圆=π•OA2-π•OP2=π(OA2-OP2)=25π;
(2) 作OE⊥CD于E,如图②,
∵AB=10,AC=2,
∴AE=
AB=5,
∴CE=AE-AC=5-2=3,
∵OA2=OE2+AE2,OC2=OE2+CE2,
∴圆环的面积=S大圆-S小圆=π•OA2-π•OC2=π(AE2-CE2)=(25-9)π=16π.
故答案为16π.

∵直线l与小圆相切于点P,
∴OP⊥AB,
∴AP=BP;
② 连结OA,如图①,AP=BP=
| 1 |
| 2 |
在Rt△OPA中,OA2-OP2=AP2=25,
∴圆环的面积=S大圆-S小圆=π•OA2-π•OP2=π(OA2-OP2)=25π;
(2) 作OE⊥CD于E,如图②,
∵AB=10,AC=2,
∴AE=
| 1 |
| 2 |
∴CE=AE-AC=5-2=3,
∵OA2=OE2+AE2,OC2=OE2+CE2,
∴圆环的面积=S大圆-S小圆=π•OA2-π•OC2=π(AE2-CE2)=(25-9)π=16π.
故答案为16π.
看了 我们知道,求圆环的面积可以转...的网友还看了以下:
(2006•潍坊模拟)图示鸟卵的解剖结构,据图回答(1)卵黄上的白色小点[1]叫做.在发育过程,[ 2020-05-17 …
图示鸟卵的解剖结构,据图回答(1)卵黄上的白色小点[1]叫做.在发育过程,[1]是形成的部位.(2 2020-05-17 …
图为鸟卵的解剖结构,据图回答:(1)卵黄上的白色小点[1]叫做.在发育过程,[1]是形成的部位.( 2020-05-17 …
如图为鸟卵的解剖结构,据图回答:(1)卵黄上的白色小点[1]叫做.(2)能够为胚胎发育提供养料的是 2020-05-17 …
如图为鸟卵的解剖结构,据图回答:(1)卵黄上的白色小点[1]叫做,其中含有,将来形成进而发育成雏鸟 2020-05-17 …
读“风的形成示意图”,回答下列问题。(每空或每一小点1分,共15分)(1)该图表示(填近地面或高空) 2020-12-15 …
下图为鸟卵的解剖结构,据图回答:(1)卵黄上的白色小点[1]叫做。在发育过程,[1]是形成的部位。( 2020-12-17 …
如图为鸟卵的解剖结构,据图回答:(1)卵黄上的白色小点[1]叫做.在发育过程,[1]是形成胚胎的部位 2020-12-17 …
如图为鸟卵的解剖结构,据图回答问题.(1)卵黄上的白色小点1叫做.(2)2是、3是,两者与1共同构成 2020-12-17 …
如图为鸟卵的解剖结构,据图回答:(1)卵黄上的白色小点[1]叫做,其中含有,将来形成胚胎进而发育成雏 2020-12-17 …