早教吧作业答案频道 -->数学-->
已知在平行四边形ABCD中,AE⊥BC于E点,DF平分∠ADC交线段AE于F点.(1)如图1,若AE=AD,求证:CD=AF+BE;(2)如图2,若AE:AD=a:b,试探究线段CD、AF、BE之间所满足的等量关系,请直接写出你
题目详情
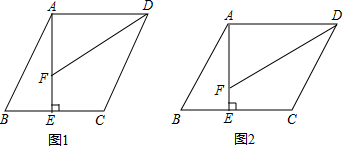
已知在平行四边形ABCD中,AE⊥BC于E点,DF平分∠ADC 交线段AE于F点.
(1)如图1,若AE=AD,求证:CD=AF+BE;
(2)如图2,若AE:AD=a:b,试探究线段CD、AF、BE之间所满足的等量关系,请直接写出你的结论.
(1)如图1,若AE=AD,求证:CD=AF+BE;
(2)如图2,若AE:AD=a:b,试探究线段CD、AF、BE之间所满足的等量关系,请直接写出你的结论.

▼优质解答
答案和解析
(1)证明:延长EA到G,使得AG=BE,连接DG,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,
∵AE⊥BC于点E,
∴∠AEB=∠AEC=90°,
∴∠AEB=∠DAG=90°,
∴∠DAG=90°,
在△ABE和△DGA中
,
∴△ABE≌△DGA,
∴∠1=∠2,DG=AB,∠B=∠G,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC,
∵∠B+∠1=∠ADC+∠2=90°,∠3=∠4,
∴∠GDF=90°-∠4,∠GFD=90°-∠3,
∴∠GDF=∠GFD,
∴GF=GD=AB=CD,
∵GF=AF+AG=AF+BE,
∴CD=AF+BE;
(2)bCD=aAF+bBE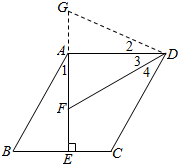
理由是:延长EA到G,使得
=
,连接DG,
即AG=
BE,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,
∵AE⊥BC于点E,
∴∠AEB=∠AEC=90°,
∴∠AEB=∠DAG=90°,
∴∠DAG=90°,
即∠AEB=∠GAD=90°,
∵
=
=
,
∴△ABE∽△DGA,
∴∠1=∠2,
=
,
∴∠GFD=90°-∠3,
∵DF平分∠ADC,
∴∠3=∠4,
∴∠GDF=∠2+∠3=∠1+∠4=180°-∠FAD-∠3=90°-∠3.
∴∠GDF=∠GFD,
∴DG=GF,
∵
=
,AB=CD(已证),
∴bCD=aDG=a(
BE+AF),
即 bCD=aAF+bBE.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,
∵AE⊥BC于点E,
∴∠AEB=∠AEC=90°,
∴∠AEB=∠DAG=90°,
∴∠DAG=90°,
在△ABE和△DGA中
|
∴△ABE≌△DGA,
∴∠1=∠2,DG=AB,∠B=∠G,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC,
∵∠B+∠1=∠ADC+∠2=90°,∠3=∠4,
∴∠GDF=90°-∠4,∠GFD=90°-∠3,
∴∠GDF=∠GFD,
∴GF=GD=AB=CD,
∵GF=AF+AG=AF+BE,
∴CD=AF+BE;
(2)bCD=aAF+bBE

理由是:延长EA到G,使得
| BE |
| AG |
| a |
| b |
即AG=
| b |
| a |
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,
∵AE⊥BC于点E,
∴∠AEB=∠AEC=90°,
∴∠AEB=∠DAG=90°,
∴∠DAG=90°,
即∠AEB=∠GAD=90°,
∵
| AE |
| AD |
| BE |
| AG |
| a |
| b |
∴△ABE∽△DGA,
∴∠1=∠2,
| AB |
| DG |
| a |
| b |
∴∠GFD=90°-∠3,
∵DF平分∠ADC,
∴∠3=∠4,
∴∠GDF=∠2+∠3=∠1+∠4=180°-∠FAD-∠3=90°-∠3.
∴∠GDF=∠GFD,
∴DG=GF,
∵
| AB |
| DG |
| a |
| b |
∴bCD=aDG=a(
| b |
| a |
即 bCD=aAF+bBE.
看了 已知在平行四边形ABCD中,...的网友还看了以下:
探究在线八年级北师大版期中测试题一.已知正方形ABCD,E是AB的中点,过点B作BF⊥AE于F,B 2020-06-08 …
求助2018年探究在线高效课堂七年级英语下册的答案! 2020-06-14 …
求助2018年探究在线高效课堂九年级数学下册的答案! 2020-06-14 …
谁有2018年探究在线高效课堂七年级数学下册北师大版的答案? 2020-06-14 …
求助2018年探究在线高效课堂七年级生物下册北师大版的答案! 2020-06-14 …
探究在线青春的美丽既印在相纸上,也印在我们的心坎上。在我们心灵的相册里,既有男生也有女生。为引导男 2020-06-21 …
求助2018年探究在线高效课堂七年级生物下册冀少版的答案! 2020-07-01 …
帮帮忙,2018年探究在线高效课堂七年级数学下册沪科版这本答案谁有? 2020-07-02 …
英语翻译“基于在线监测的机动车尾气污染时空分布研究”在线监测;机动车尾气污染;时空分布;希望不要机械 2020-12-13 …
探究在线“民以食为天,食以安为先”。然而近几年来,食品安全丑闻此起彼伏,从苏丹红到三聚氰胺,从地沟油 2021-01-01 …