早教吧作业答案频道 -->数学-->
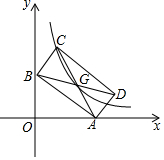
如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=3,OB=2,对角线AC、BD交于点G,若曲线y=kx(x>0)经过点C、G,则k=.
题目详情
如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=3,OB=2,对角线AC、BD交于点G,若曲线y=
(x>0)经过点C、G,则k=___.
| k |
| x |

▼优质解答
答案和解析
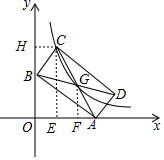 如图,分别过C、G两点作x轴的垂线,交x轴于点E、F,
如图,分别过C、G两点作x轴的垂线,交x轴于点E、F,
∴CE∥GF,
设C(m.n),
∵四边形ABCD是矩形,
∴AG=CG,
∴GF=
CE,EF=
(3-m),
∴OF=
(3-m)+m=
+
m,
∴G(
,
n),
∵曲线y=
(x>0)经过点C、G,
∴mn=
×
n,
解得m=1,
作CH⊥y轴于H,
∴CH=1,
∵∠ABC=90°,
∴∠CBH+∠ABO=90°,
∵∠OAB+∠ABO=90°,
∴∠OAB=∠CBH,
∵∠AOB=∠BHC=90°,
∴△AOB∽△BHC,
∴
=
,即
=
,
∴BH=
,
∴OH=
+2=
,
∴C(1,
),
∴k=1×
=
;
故答案为
.
 如图,分别过C、G两点作x轴的垂线,交x轴于点E、F,
如图,分别过C、G两点作x轴的垂线,交x轴于点E、F,∴CE∥GF,
设C(m.n),
∵四边形ABCD是矩形,
∴AG=CG,
∴GF=
| 1 |
| 2 |
| 1 |
| 2 |
∴OF=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴G(
| 3+m |
| 2 |
| 1 |
| 2 |
∵曲线y=
| k |
| x |
∴mn=
| 3+m |
| 2 |
| 1 |
| 2 |
解得m=1,
作CH⊥y轴于H,
∴CH=1,
∵∠ABC=90°,
∴∠CBH+∠ABO=90°,
∵∠OAB+∠ABO=90°,
∴∠OAB=∠CBH,
∵∠AOB=∠BHC=90°,
∴△AOB∽△BHC,
∴
| BH |
| OA |
| CH |
| OB |
| BH |
| 3 |
| 1 |
| 2 |
∴BH=
| 3 |
| 2 |
∴OH=
| 3 |
| 2 |
| 7 |
| 2 |
∴C(1,
| 7 |
| 2 |
∴k=1×
| 7 |
| 2 |
| 7 |
| 2 |
故答案为
| 7 |
| 2 |
看了 如图,矩形ABCD的两个顶点...的网友还看了以下:
已知直线Y=KX+B经过点K,3和1,K.则K值? 2020-04-25 …
一个二次函数,其图象由抛物线y=1/2x^2向右平移一个单位,再向上平移k个单位(k>0)得到,平 2020-04-26 …
求一道数学题的解答、是德州2011年一模的两点抛物线M:y^2=ax的焦点F(1,0),过点K(- 2020-04-27 …
已知一次函数y=x+b经过点(k,3)和(1,k)则K的值为求解题思路... 2020-05-21 …
.已知抛物线y^2=4x的焦点F,过点K(-1,0)的直线与抛物线交与A.B两点,点A关于x轴的对 2020-06-21 …
已知直线y=2x+3,y=-2x-5,y=kx-7/2都经过同一点.(1)求k的值;(2)求经过( 2020-06-28 …
如图,抛物线C1:y=a(x-1)2经过点A(3,4).(1)求a的值;(2)将抛物线C1向下平移 2020-07-09 …
有一数轴原点为O,点A所对应的数是-112,点A沿数轴匀速平移,经过原点到达点B1如果OA=OB. 2020-07-10 …
在四边形abcd中角dab等于角abc等于90度ad等于ab等于4,bc等于8,点n从a出发,沿a 2020-07-30 …
(2014•泉州质检)已知顶点为P的抛物线C1的解析式是y=a(x-3)2(a≠0),且经过点(0, 2020-11-27 …