早教吧作业答案频道 -->数学-->
问题情境如图1,Rt△ABC中,∠ACB=90°,CD⊥AB,我们可以利用△ABC与△ACD相似证明AC2=AD•AB,这个结论我们称之为射影定理,试证明这个定理;结论运用如图2,正方形ABCD的边长为6,
题目详情
【问题情境】如图1,Rt△ABC中,∠ACB=90°,CD⊥AB,我们可以利用△ABC与△ACD相似证明AC2=AD•AB,这个结论我们称之为射影定理,试证明这个定理;
【结论运用】如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
(1)试利用射影定理证明△BOF∽△BED;
(2)若DE=2CE,求OF的长.
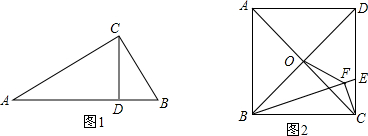
【结论运用】如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
(1)试利用射影定理证明△BOF∽△BED;
(2)若DE=2CE,求OF的长.
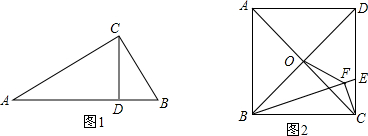
▼优质解答
答案和解析
【问题情境】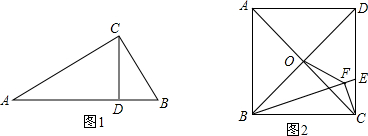
证明:如图1,
∵CD⊥AB,
∴∠ADC=90°,
而∠CAD=∠BAC,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,
∴AC2=AD•AB;
【结论运用】
(1)证明:如图2,
∵四边形ABCD为正方形,
∴OC⊥BO,∠BCD=90°,
∴BC2=BO•BD,
∵CF⊥BE,
∴BC2=BF•BE,
∴BO•BD=BF•BE,
即
=
,
而∠OBF=∠EBD,
∴△BOF∽△BED;
(2)∵BC=CD=6,
而DE=CE,
∴DE=4,CE=2,
在Rt△BCE中,BE=
=2
,
在Rt△OBC中,OB=
BC=3
,
∵△BOF∽△BED,
∴
=
,即
=
,
∴OF=
.
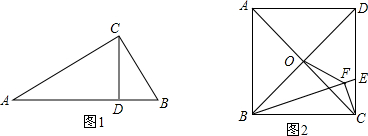
证明:如图1,
∵CD⊥AB,
∴∠ADC=90°,
而∠CAD=∠BAC,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,
∴AC2=AD•AB;
【结论运用】
(1)证明:如图2,
∵四边形ABCD为正方形,
∴OC⊥BO,∠BCD=90°,
∴BC2=BO•BD,
∵CF⊥BE,
∴BC2=BF•BE,
∴BO•BD=BF•BE,
即
| BO |
| BE |
| BF |
| BD |
而∠OBF=∠EBD,
∴△BOF∽△BED;
(2)∵BC=CD=6,
而DE=CE,
∴DE=4,CE=2,
在Rt△BCE中,BE=
| 22+62 |
| 10 |
在Rt△OBC中,OB=
| ||
| 2 |
| 2 |
∵△BOF∽△BED,
∴
| OF |
| DE |
| BO |
| BE |
| OF |
| 4 |
3
| ||
2
|
∴OF=
6
| ||
| 5 |
看了 问题情境如图1,Rt△ABC...的网友还看了以下:
两个有理数相加.减.乘.除,结果一定是有理数吗?两个无理数相加.减.乘.除,结果一定是无理数吗?说 2020-05-13 …
下列说法中,错误的个数是()①两个单项式相加,结果一定是单项式②两个单项式相乘,结果一定是单项式③ 2020-05-13 …
统计分析的重要特征之一是()。A.经验方法与数字方法相结合B.定量分析与经济分析相结合C.定量分析 2020-05-21 …
两个有理数相加,相减,相除,相乘,结果一定是有理数吗?说明理由.两个无理数相加,相减,相除,相乘, 2020-07-31 …
(1)两个有理数相加、相减、相乘、相除,结果一定还是有理数吗?说明理由.(2)两个无理数相加、相减 2020-07-31 …
一般相似三角形的判定方法有哪几种?如何灵活选用?请你填一填,补充完成这份小结.相似三角形的判定一共 2020-08-01 …
群落空间结构决定于两个要素,即群落中各物种的及相同生活型的物种所组成的层片,群落空间结构决定于两个要 2020-11-05 …
1、有两个相等的三角形是().可以简述为()2、先假设命题的结论不成立,然后推导出与定义、公理、已证 2020-12-23 …
两条一级结构相同的肽链所形成的空间结构必定一样吗?或者说一级结构相同的肽链是不是就是同种蛋白质有没有 2021-01-01 …
组成和结构决定性质,组成和结构上的某些相同必然会带来某些性质上的相似.下列结论不正确的是()A.酸具 2021-01-22 …