早教吧作业答案频道 -->数学-->
已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F、Q为斜边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是,QE与QF的数量关系
题目详情
已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F、Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是___,QE与QF的数量关系是___;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
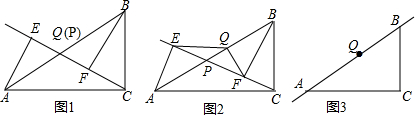
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是___,QE与QF的数量关系是___;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.

▼优质解答
答案和解析
(1)如图1,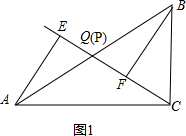
当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是AE=BF,
理由是:∵Q为AB的中点,
∴AQ=BQ,
∵AE⊥CQ,BF⊥CQ,
∴AE∥BF,∠AEQ=∠BFQ=90°,
在△AEQ和△BFQ中
∴△AEQ≌△BFQ,
∴QE=QF,
故答案为:AE∥BF,QE=QF;
(2)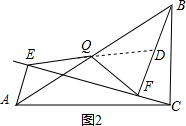
QE=QF,
证明:延长EQ交BF于D,
∵由(1)知:AE∥BF,
∴∠AEQ=∠BDQ,
在△AEQ和△BDQ中
∴△AEQ≌△BDQ,
∴EQ=DQ,
∵∠BFE=90°,
∴QE=QF;,
(3)当点P在线段BA(或AB)的延长线上时,此时(2)中的结论成立,
证明:延长EQ交FB于D,如图3,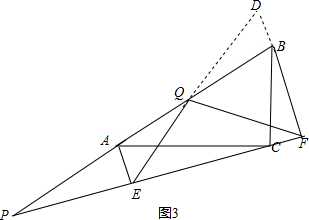
∵由(1)知:AE∥BF,
∴∠AEQ=∠BDQ,
在△AEQ和△BDQ中
∴△AEQ≌△BDQ,
∴EQ=DQ,
∵∠BFE=90°,
∴QE=QF.

当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是AE=BF,
理由是:∵Q为AB的中点,
∴AQ=BQ,
∵AE⊥CQ,BF⊥CQ,
∴AE∥BF,∠AEQ=∠BFQ=90°,
在△AEQ和△BFQ中
|
∴△AEQ≌△BFQ,
∴QE=QF,
故答案为:AE∥BF,QE=QF;
(2)

QE=QF,
证明:延长EQ交BF于D,
∵由(1)知:AE∥BF,
∴∠AEQ=∠BDQ,
在△AEQ和△BDQ中
|
∴△AEQ≌△BDQ,
∴EQ=DQ,
∵∠BFE=90°,
∴QE=QF;,
(3)当点P在线段BA(或AB)的延长线上时,此时(2)中的结论成立,
证明:延长EQ交FB于D,如图3,

∵由(1)知:AE∥BF,
∴∠AEQ=∠BDQ,
在△AEQ和△BDQ中
|
∴△AEQ≌△BDQ,
∴EQ=DQ,
∵∠BFE=90°,
∴QE=QF.
看了 已知,点P是Rt△ABC斜边...的网友还看了以下:
在DNA分子的碱基组成中,因生物种类不同而异的是A.(A+T)/(G+C) B.C/GC.A/T 2020-04-06 …
关于C语言For语句下列程序执行的结果是a=1b=2;c=3;while(b<a<c){t=a;a 2020-05-17 …
有关系模式A(C,T,H,R,S),根据语义有如下函数依赖集:F={C→T,(H,R) →C, (H 2020-05-23 …
有关系模式A(C,T,H,R,s),根据语义有如下函数依赖集:F={C→T,(H,R)→C,(H,T 2020-05-24 …
如果下面的DNA双螺旋从左向右进行转录,指出那条链是编码链.并写出转录产物的顺序?5’-A-T-C 2020-06-26 …
用a表示工作效率,t表示工作时间,c表示工作总量,写出已知工作总量和工作时间,求工效的公式是[]A 2020-07-26 …
在平面a内,若直线a⊥c,直线b⊥c,则a∥b;在空间,若直线a⊥c,直线b⊥c,则直线a与直线b不 2020-12-28 …
求解一道大学物理题?请各位i给出详细步骤及答案,万分感谢!在X轴上作变加速直线运动的质点,已知其加速 2021-01-06 …
n元二次型x^T×A×x正定,则存在可逆矩阵C,使得A=C^T×C怎么推出来的? 2021-02-05 …
求三阶矩阵(a,-1,ax-y)T(1,a,x+ay)T(b,c,bx+cy)T的秩抄错了,原题是( 2021-02-10 …