早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,直线AB与x轴交于点A(-6,0),与y轴交于点B(0,6).(1)求△ABO的面积;(2)D为OA延长线上一动点,以BD为直角边作等腰直角三角形BDE,连接EA,求直线EA与y轴交
题目详情
在平面直角坐标系xOy中,直线AB与x轴交于点A(-6,0),与y轴交于点B(0,6).
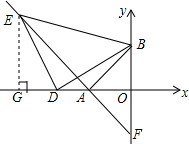
(1)求△ABO的面积;
(2)D为OA延长线上一动点,以BD为直角边作等腰直角三角形BDE,连接EA,求直线EA与y轴交点F的坐标.

(1)求△ABO的面积;
(2)D为OA延长线上一动点,以BD为直角边作等腰直角三角形BDE,连接EA,求直线EA与y轴交点F的坐标.
▼优质解答
答案和解析
(1)∵直线AB与x轴交于A(-6,0),与y轴交于B(0,6),即OA=OB=6,
∴S△ABO=
×6×6=18;
(2)作EG⊥x轴于G,可得∠EGD=∠DOB=90°,
∵△EDB为等腰直角三角形,
∴ED=BD,∠BDE=90°,
∵∠DEG+∠EDG=90°,∠EDG+∠BDO=90°,
∴∠DEG=∠BDO,
在△DEF和△BDO中,
,
∴△DEF≌△BDO(AAS),
∴EG=OD,DG=OB=6,
设D(-d,0),d>6,则G(-d-6,0),E(-d-6,d),
设直线EA的解析式为y=kx+b,则
,
解得:k=-1,b=-6,
∴直线EA的解析式为y=-x-6,
令x=0,得到y=-6,即F(0,-6).
∴S△ABO=
| 1 |
| 2 |
(2)作EG⊥x轴于G,可得∠EGD=∠DOB=90°,
∵△EDB为等腰直角三角形,
∴ED=BD,∠BDE=90°,
∵∠DEG+∠EDG=90°,∠EDG+∠BDO=90°,
∴∠DEG=∠BDO,
在△DEF和△BDO中,
|
∴△DEF≌△BDO(AAS),
∴EG=OD,DG=OB=6,
设D(-d,0),d>6,则G(-d-6,0),E(-d-6,d),
设直线EA的解析式为y=kx+b,则
|
解得:k=-1,b=-6,
∴直线EA的解析式为y=-x-6,
令x=0,得到y=-6,即F(0,-6).
看了 在平面直角坐标系xOy中,直...的网友还看了以下:
如图所示,一条形磁铁原来做自由落体运动,当它通过闭合线圈回路时,其运动情况是()A.接近线圈和离开 2020-07-29 …
几何题,单选题,只提交答案.不需要附件.例如:1.A2.B......1.当直线平行于某投影面时, 2020-08-02 …
电压U线=660V,有功功率P1=8.2KW,功率因数cosΦ=0.83,求电动机的相,线的电流?有 2020-12-13 …
对称星形连接负载,每相复阻抗Z=(24+j32)Ω,接于线电压U1=380V的三相电源上,求各相电流 2020-12-25 …
电压U线=660V,有功功率P1=8.2KW,功率因数cosΦ=0.83,求电动机的相,线的电流?有 2020-12-25 …
有一对称三相负载采用星形接法,接于线电压U1=300V,的三相对称交流电源上,每相等效电阻R=40欧 2020-12-25 …
对称三相电阻炉作三角形连接,每项电阻R=38,接于线电压Ut=38V的对称(后见补充)三相电源,试求 2020-12-25 …
如图所示,平行板电容器的两极板A、B接于电池两极,一带正电的小球悬挂在电容器内部,闭合S,电容器充电 2021-01-02 …
如图所示,平行板电容器的两极板A、B接于电池两极,一带正电的小球悬挂在电容器内部,闭合S,电容器充电 2021-01-02 …
电工题.急有一三相对称负载,每项负载的电阻是80欧,电抗是60欧,在下列两种情况下,请求负载上通过的 2021-01-14 …