早教吧作业答案频道 -->数学-->
如图①,在△ABC中∠ACB=90°,AC=BC,M是AB中点,P为AB上一动点(P不与A、B重合),PE⊥AC于点E,PF⊥BC于点F.(1)求证:ME=MF,ME⊥MF;(2)如点P移动至AB的延长线上,如图②,是否仍有如上结
题目详情
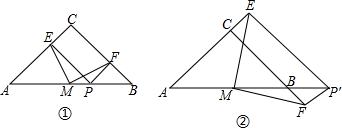
如图①,在△ABC中∠ACB=90°,AC=BC,M是AB中点,P为AB上一动点(P不与A、B重合),PE⊥AC于点E,PF⊥BC于点F.
(1)求证:ME=MF,ME⊥MF;
(2)如点P移动至AB的延长线上,如图②,是否仍有如上结论?请予以证明.
(1)求证:ME=MF,ME⊥MF;
(2)如点P移动至AB的延长线上,如图②,是否仍有如上结论?请予以证明.

▼优质解答
答案和解析
证明:(1)连接CM,
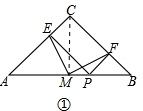
∵∠ACB=90°,PE⊥AC,PF⊥BC,
∴四边形CEFP是矩形,
∴FP=CE,
∵∠ACB=90°,AC=BC
∴∠ACM=∠B=45°,CM⊥AB,CM=BM,
∵PF⊥BC,
∴△BFP为等腰直角三角形,
∴PF=BF,
∴CE=PF=BF,
在△ECM和△FBM中,
,
∴△ECM≌△FBM(SAS),
∴EM=FM,∠EMC=∠FMB,
∵∠FMB+∠CMF=90°,
∴∠EMC+∠CMF=90°.即EM⊥FM;
(2)连接CM,
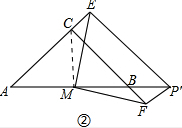
∵P'F⊥CF,P'E⊥CE,
∴四边形CEP'F是矩形,∴P'F=CE,
∵∠ACB=90°,AC=BC,
∴∠CBM=∠BCM=45°,BM=BM,CM⊥AB,
∴∠MBF=∠MCE=135°,∠FBP'=45°,
∴BF=FP',
在△CEM和△BFM中,
,
∴△CEM≌△BFM(SAS),
∴ME=MF,∠CME=∠BMF,
∵∠CMB+∠EMB=90°,
∴∠EMB+∠FMB=∠EMF=90°,即EM⊥FM.

∵∠ACB=90°,PE⊥AC,PF⊥BC,
∴四边形CEFP是矩形,
∴FP=CE,
∵∠ACB=90°,AC=BC
∴∠ACM=∠B=45°,CM⊥AB,CM=BM,
∵PF⊥BC,
∴△BFP为等腰直角三角形,
∴PF=BF,
∴CE=PF=BF,
在△ECM和△FBM中,
|
∴△ECM≌△FBM(SAS),
∴EM=FM,∠EMC=∠FMB,
∵∠FMB+∠CMF=90°,
∴∠EMC+∠CMF=90°.即EM⊥FM;
(2)连接CM,

∵P'F⊥CF,P'E⊥CE,
∴四边形CEP'F是矩形,∴P'F=CE,
∵∠ACB=90°,AC=BC,
∴∠CBM=∠BCM=45°,BM=BM,CM⊥AB,
∴∠MBF=∠MCE=135°,∠FBP'=45°,
∴BF=FP',
在△CEM和△BFM中,
|
∴△CEM≌△BFM(SAS),
∴ME=MF,∠CME=∠BMF,
∵∠CMB+∠EMB=90°,
∴∠EMB+∠FMB=∠EMF=90°,即EM⊥FM.
看了 如图①,在△ABC中∠ACB...的网友还看了以下:
设[E:F]=P,P是素数,a属于E\F.证明:F(a)=E.先到先得. 2020-04-06 …
在△ABC中,过B,C分别作∠BAC的平分线的垂线,E,F为垂足,AD⊥BC于D,M为BC中点.求 2020-04-25 …
2道几何题已知:P是正方形ABCD对角线BD上一点.PE垂直DC.PF垂直BC.E.F分别为垂足. 2020-05-13 …
如图,BD是平行四边形ABCD的对角线,E,F在BD上,要使四边形AECF是平行四边形,需添加什么 2020-05-15 …
如图,AD是△ABC的角平分线,E,F分别是AC,AB上的两点,CE=BF,求证:S△DCE=S△ 2020-05-19 …
AB是半圆O的直径,OC垂直AB,圆M与OC,OB和圆O都相切,切点分别为D,E,F,证:A,D, 2020-06-03 …
全等三角形中线倍长法:ad是三角形abc的中线,e,f分别在ab,ac上,且de垂直df,则be, 2020-07-01 …
如图三角形ABC中,AD是角BAC的平分线,E.F分别是AB,AC上的点,且角EDF+角BAF=1 2020-07-18 …
证明题(有关内心)设三角形ABC的内心为I,三角形ABC内一点P在BC,CA,AB上的射影分别为D 2020-07-30 …
PA,PB是圆0两切线,PCD是割线,E,F分别在AB,AD上,CE=CF,求证:CF与PA互相平行 2020-12-05 …