早教吧作业答案频道 -->数学-->
在数学探究课上,老师出示了这样的探究问题,请你一起来探究:已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边三角形ACE和BCD,联结AD、BE交于点P.(1)如图1,当
题目详情
在数学探究课上,老师出示了这样的探究问题,请你一起来探究:
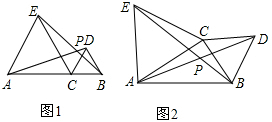
已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边三角形ACE和BCD,联结AD、BE交于点P.
(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是:___.
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.
(3)在(2)的条件下,∠APE的大小是否随着∠ACB的大小的变化而发生变化,若变化,写出变化规律,若不变,请求出∠APE的度数.

已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边三角形ACE和BCD,联结AD、BE交于点P.
(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是:___.
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.
(3)在(2)的条件下,∠APE的大小是否随着∠ACB的大小的变化而发生变化,若变化,写出变化规律,若不变,请求出∠APE的度数.
▼优质解答
答案和解析
(1)∵△ACE、△CBD均为等边三角形,
∴AC=EC,CD=CB,∠ACE=∠BCD,
∴∠ACD=∠ECB;
在△ACD与△ECB中,
,
∴△ACD≌△ECB(SAS),
∴AD=BE,
故答案为AD=BE.
(2)AD=BE成立.
证明:∵△ACE和△BCD是等边三角形
∴EC=AC,BC=DC,
∠ACE=∠BCD=60°,
∴∠ACE+∠ACB=∠BCD+∠ACB,即∠ECB=∠ACD;
在△ECB和△ACD中,
,
∴△ECB≌△ACD(SAS),
∴BE=AD.
(3))∠APE不随着∠ACB的大小发生变化,始终是60°.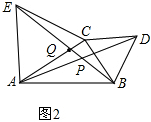
如图2,设BE与AC交于Q,
由(2)可知△ECB≌△ACD,
∴∠BEC=∠DAC
又∵∠AQP=∠EQC,∠AQP+∠QAP+∠APQ=∠EQC+∠CEQ+∠ECQ=180°
∴∠APQ=∠ECQ=60°,即∠APE=60°.
∴AC=EC,CD=CB,∠ACE=∠BCD,
∴∠ACD=∠ECB;
在△ACD与△ECB中,
|
∴△ACD≌△ECB(SAS),
∴AD=BE,
故答案为AD=BE.
(2)AD=BE成立.
证明:∵△ACE和△BCD是等边三角形
∴EC=AC,BC=DC,
∠ACE=∠BCD=60°,
∴∠ACE+∠ACB=∠BCD+∠ACB,即∠ECB=∠ACD;
在△ECB和△ACD中,
|
∴△ECB≌△ACD(SAS),
∴BE=AD.
(3))∠APE不随着∠ACB的大小发生变化,始终是60°.

如图2,设BE与AC交于Q,
由(2)可知△ECB≌△ACD,
∴∠BEC=∠DAC
又∵∠AQP=∠EQC,∠AQP+∠QAP+∠APQ=∠EQC+∠CEQ+∠ECQ=180°
∴∠APQ=∠ECQ=60°,即∠APE=60°.
看了 在数学探究课上,老师出示了这...的网友还看了以下:
下列句于中,加点成语使用无误的一项是A、在“课内比较学”活动中.郭老师的课讲得惟妙惟肖,赢得了全班 2020-04-05 …
下列句子中,划线成语使用无误的一项是A.在“课内比较学”活动中,郭老师的课讲得惟妙惟肖,赢得了全班 2020-04-11 …
老师也难免会犯错误,我们要用最恰当方式指出,下列属于“最恰当的方式”的是A.在课堂上直截了当地指出 2020-05-15 …
老师也难免会犯错误,我们要用最恰当方式指出,下列属于“最恰当的方式”的是A.在课堂上直截了当地指出 2020-05-15 …
作者身处美丽的索溪峪,感受到的是一个字野,这在课文中指的是一种没有经过什么什么什么的美? 2020-06-26 …
下列行为属于有自尊心的表现是[]A.在课堂上受批评的李华,低着头,脸上火辣辣的B.赵蒙被几个调皮鬼起 2020-11-24 …
这又是一个谜的这在课文中指的是什么 2020-12-03 …
关于声的知识,下列说法错误的是()A.在课堂上听到老师讲话声,证明声音可以在空气中传播B.在城市通路 2020-12-05 …
关于声的知识,下列说法错误的是()A.在课堂上听到老师讲话声,证明声音可以在空气中传播B.在城市通路 2020-12-17 …
培养法律意识,养成守法观念,重在平时、重在落实,为此在实际生活中,我们应该()A.只在课上认真学习法 2020-12-21 …