如图，AB为O的直径，弦CD⊥AB于点E，点G是AD上一点，连结AG，CG．（1）试找出与∠AGC相等的角，并进行证明；（2）若AB∥DG，求证；△ACG与△ACE相似；（3）若OE=BE，求∠AGC的度数．

Question

如图，AB为 O的直径，弦CD⊥AB于点E，点G是

AD

上一点，连结AG，CG．

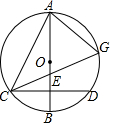
（1）试找出与∠AGC相等的角，并进行证明；
（2）若AB∥DG，求证；△ACG与△ACE相似；
（3）若OE=BE，求∠AGC的度数．

Answer 1

（1）结论：∠ACE=∠AGC．理由如下：
如图1中，连接AD．

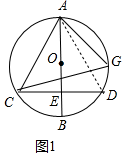
∵AB是直径，AB⊥CD，
∴EC=ED，
∴AD=AC，
∴∠ACE=∠ADC，
∵∠AGC=∠ADC，
∴∠ACE=∠AGC．

（2）证明：如图2中，

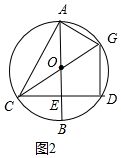
∵DG∥AB，
∴∠AEC=∠CDG=90°，
∴CG是直径，
∴∠CAG=90°，
∵∠CAG=∠AEC=90°，∠AGC=∠ACE，
∴△ACG∽△EAC．

（3） 如图3中，连接OC、BC．

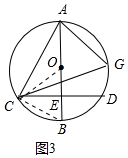
∵OE=EB，CE⊥OB，
∴CO=CB=OB，
∴△OBC是等边三角形，
∴∠B=60°，
∴∠AGC=∠B=60°．