早教吧作业答案频道 -->数学-->
如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.(1)判断四边形ACGD的形状,并说明理由
题目详情
如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.
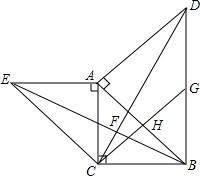
(1)判断四边形ACGD的形状,并说明理由.
(2)求证:BE=CD,BE⊥CD.

(1)判断四边形ACGD的形状,并说明理由.
(2)求证:BE=CD,BE⊥CD.
▼优质解答
答案和解析
(1) ∵△ABC是等腰直角三角形,∠ACB=90°,
∴AB=
BC,
∵△ABD和△ACE均为等腰直角三角形,
∴BD=
AB=BC
×
×BC=2BC,
∵G为BD的中点,
∴BG=
BD=BC,
∴△CBG为等腰直角三角形,
∴∠CGB=45°,
∵∠ADB=45°,
AD∥CG,
∵∠ABD=45°,∠ABC=45°
∴∠CBD=90°,
∵∠ACB=90°,
∴∠CBD+∠ACB=180°,
∴AC∥BD,
∴四边形ACGD为平行四边形;
(2)证明:∵∠EAB=∠EAC+∠CAB=90°+45°=135°,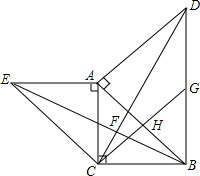
∠CAD=∠DAB+∠BAC=90°+45°=135°,
∴∠EAB=∠CAD,
在△DAC与△BAE中,
,
∴△DAC≌△BAE,
∴BE=CD;
∵∠EAC=∠BCA=90°,EA=AC=BC,
∴四边形ABCE为平行四边形,
∴CE=AB=AD,
在△BCE与△CAD中,
,
∴△BCE≌△CAD,
∴∠CBE=∠ACD,
∵∠ACD+∠BCD=90°,
∴∠CBE+∠BCD=90°,
∴∠CFB=90°,
即BE⊥CD.
∴AB=
| 2 |
∵△ABD和△ACE均为等腰直角三角形,
∴BD=
| 2 |
| 2 |
| 2 |
∵G为BD的中点,
∴BG=
| 1 |
| 2 |
∴△CBG为等腰直角三角形,
∴∠CGB=45°,
∵∠ADB=45°,
AD∥CG,
∵∠ABD=45°,∠ABC=45°
∴∠CBD=90°,
∵∠ACB=90°,
∴∠CBD+∠ACB=180°,
∴AC∥BD,
∴四边形ACGD为平行四边形;
(2)证明:∵∠EAB=∠EAC+∠CAB=90°+45°=135°,

∠CAD=∠DAB+∠BAC=90°+45°=135°,
∴∠EAB=∠CAD,
在△DAC与△BAE中,
|
∴△DAC≌△BAE,
∴BE=CD;
∵∠EAC=∠BCA=90°,EA=AC=BC,
∴四边形ABCE为平行四边形,
∴CE=AB=AD,
在△BCE与△CAD中,
|
∴△BCE≌△CAD,
∴∠CBE=∠ACD,
∵∠ACD+∠BCD=90°,
∴∠CBE+∠BCD=90°,
∴∠CFB=90°,
即BE⊥CD.
看了 如图,△ABC是等腰直角三角...的网友还看了以下:
如图所示,在点电荷Q形成的电场中,带电粒子q仅受电场力作用,运动轨迹为MEGFN曲线,其中G点与等 2020-05-15 …
判断下列是不是命题,是命题的指出它的真假.1、在直线AB上任取一点C.2、同位角相等判断下列是不是 2020-07-23 …
如图所示,实线表示电场线,虚线表示等势线,a、b两点的电势分别为φa=-50V,φb=-20V,则 2020-07-29 …
如图,用尺规作图作“一个角等于已知角”的原理是:因为△D′O′C′≌△DOC,所以∠D′O′C′= 2020-07-31 …
一.判断1.圆的周长是直径的π(pai)倍2.圆的周长为C,半径为r,那么圆周率π等于C除以2r3 2020-08-01 …
出错了,为什么?Console.WriteLine("请输入成绩");intcj=Convert. 2020-08-02 …
c语言判断两个字符串相等判断字符串s1与字符串s2相等,应当使用:c.\x05A)if(s1=s2) 2020-11-07 …
如果c为字符型变量,下面可以判断c是否为空格10、如果c为字符型变量,下面可以判断c是否为空格.A) 2020-11-07 …
下列现象属于生物主要对温度表现出适应性的实例是()A.陆生鸟类和哺乳类肾脏的肾小管和集合管很长B.沙 2020-12-23 …
某地区3月1日至30日的天气情况及晚间空间温度统计如表,比如,根据表中数据可知3月1日无雨,且当日晚 2021-01-01 …