早教吧作业答案频道 -->数学-->
在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DE⊥AB,垂足为E,连接AD,将△DEB沿直线DE翻折得到△DEF,点B落在射线BA上的F处.(1)求证:△DEB∽△ACB
题目详情
在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DE⊥AB,垂足为E,连接AD,将△DEB沿直线DE翻折得到△DEF,点B落在射线BA上的F处.
(1)求证:△DEB∽△ACB;
(2)当点F与点A重合时(如图①),求线段BD的长;
(3)设BD=x,AF=y,求y关于x的函数解析式,并判断是否存在这样的点D,使AF=FD?若存在,请求出x的值;若不存在,请说明理由.
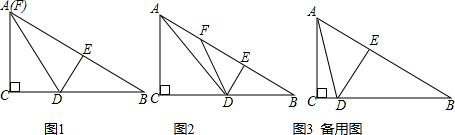
(1)求证:△DEB∽△ACB;
(2)当点F与点A重合时(如图①),求线段BD的长;
(3)设BD=x,AF=y,求y关于x的函数解析式,并判断是否存在这样的点D,使AF=FD?若存在,请求出x的值;若不存在,请说明理由.

▼优质解答
答案和解析
(1)证明:∵DE⊥AB,∴∠DEB=90°,∴∠ACB=∠DEB,又∠B=∠B,∴△DEB∽△ACB;(2)∵∠ACB=90°,AC=6,BC=8,∴AB=AC2+BC2=10,由翻转变换的性质可知,BE=AE=12AB=5,∵△DEB∽△ACB,∴BDBA=BEBC,即BD10=58...
看了 在Rt△ABC中,∠ACB=...的网友还看了以下:
A、B、C、D、E和F六人一圆桌坐下.B是坐在A右边的第二人.C是坐在F右边的第二人.D坐在E的正 2020-04-09 …
A、B、C、D、E和F六人一圆桌坐下.B是坐在A右边的第二人.C是坐在F右边的第二人.D坐在E的正 2020-04-09 …
分子式为C8H16O2的酯A,能在酸性条件下水解生成B和C,且B在一定条件下能氧化成D.D与C互为 2020-05-13 …
有A、B、C、D、E五种物质.A的水溶液加入一种黑色粉末B可迅速产生一种气体C.D可在C中烈燃烧, 2020-07-03 …
如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3.点D为BC边上一点 2020-07-10 …
称量有腐蚀性的固体药品时,应该将药品()A.放在左边托盘上B.先放在烧杯中,再放在左边托盘上C.放 2020-07-13 …
三角形ABC为等边三角形D为AC上一点BD的垂直平分线交AB于点E交BC于点F1.当D在AC上移动 2020-08-03 …
读经纬线图,回答下列问题(1)写出下面各点的经纬度:A.B.C.D..(2)四点中,位于北半球的是; 2020-12-04 …
在回旋加速器中()A.高频电源产生的电场用来加速带电粒子B.D形盒内有匀强磁场,两D形盒之间的窄缝有 2020-12-22 …
(2014•通辽)读我国某区域图,下列描述正确的是()A.图中A是黄河,B是澜沧江,C是长江B.A、 2020-12-27 …