早教吧作业答案频道 -->数学-->
已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.(1)若直线AB过焦点F,求抛物线C的方程;(2)若QA⊥QB,求p的
题目详情
已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.
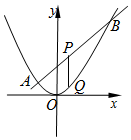
(1)若直线AB过焦点F,求抛物线C的方程;
(2)若QA⊥QB,求p的值.

(1)若直线AB过焦点F,求抛物线C的方程;
(2)若QA⊥QB,求p的值.
▼优质解答
答案和解析
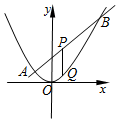 (1)根据题意,直线2x-y+2=0与y轴的交点为(0,2),
(1)根据题意,直线2x-y+2=0与y轴的交点为(0,2),
则F(0,2),
∴抛物线C的方程为x2=8y;
(2)由
得:x2-4px-4p=0,
设A(x1,y1),B(x2,y2),则x1+x2=4p,x1x2=-4p,
∴Q(2p,2p),∵QA⊥QB,则
•
=0,
(x1-2p)(x2-2p)+(y1-2p)(y2-2p)=0,
(x1-2p)(x2-2p)+(2x1+2-2p)(2x2+2-2p)=0,
5x1x2+(4-6p)(x1+x2)+8p2-8p+4=0,
代入得4p2+3p-1=0,解得p=
或p=-1(舍去)
∴p=
.
 (1)根据题意,直线2x-y+2=0与y轴的交点为(0,2),
(1)根据题意,直线2x-y+2=0与y轴的交点为(0,2),则F(0,2),
∴抛物线C的方程为x2=8y;
(2)由
|
设A(x1,y1),B(x2,y2),则x1+x2=4p,x1x2=-4p,
∴Q(2p,2p),∵QA⊥QB,则
| QA |
| QB |
(x1-2p)(x2-2p)+(y1-2p)(y2-2p)=0,
(x1-2p)(x2-2p)+(2x1+2-2p)(2x2+2-2p)=0,
5x1x2+(4-6p)(x1+x2)+8p2-8p+4=0,
代入得4p2+3p-1=0,解得p=
| 1 |
| 4 |
∴p=
| 1 |
| 4 |
看了 已知抛物线C:x2=2py(...的网友还看了以下:
怎样能求出 已知圆 关于 已知点 或 已知直线 对称的 圆的方程?怎样能求出 已知圆 关于 已知点 2020-05-16 …
已知关于X的方程A剩《2X减1》=3X减2无解求A的值AX=A当A大于等于0时方程唯一的解X等于A 2020-05-16 …
在对存货实施监盘程序时,注册会计师的以下做法中不正确的是( )。A.对于已作质押的存货, 2020-05-19 …
几道数学题(坐标)1直角坐标系中,点A(-2.7)B(3.7)两点之间长是多少?2已知P(m.n) 2020-06-06 …
已知圆C与圆x2+y2-7y+10=0相交,所得公共弦平行于已知直线2x-3y-1=0,又圆C经过 2020-06-12 …
1.已知:A(2,0),|AB|=4,B点和A点在同一数轴上,求B点坐标.已知:A(0,0),|A 2020-06-14 …
1.已知{1,2}含于A真包含于{1,2,3,4,5}的集合个数是A4B6C7D92已知A={1, 2020-07-09 …
集合AB把集合{(a,b)|a属于A,b属于B}记作A×B,已知c={a}D-{1、2、3}求C× 2020-07-30 …
已知三边求作三角形,用到的基本作图是()。A.作角等于已知角B.作已知直线的垂线C.作线段等于已知 2020-08-02 …
1.已知丨x丨小于等于1,求f(x)=x^2-2axa的最小值g(a)已知丨x丨小于等于1,求f(x 2020-12-01 …