早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系xOy中,直线y=12x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-32且经过A、C两点,与x轴的另一交点为点B.(1)直接写出点B的坐标;(2)求抛物线解
题目详情
如图,在平面直角坐标系xOy中,直线y=
x+2与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-
且经过A、C两点,与x轴的另一交点为点B.
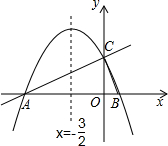
(1)直接写出点B的坐标;
(2)求抛物线解析式.
(3)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
| 1 |
| 2 |
| 3 |
| 2 |
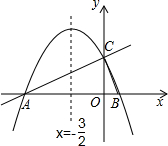
(1)直接写出点B的坐标;
(2)求抛物线解析式.
(3)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
▼优质解答
答案和解析
(1)①y=
当x=0时,y=2,当y=0时,x=-4,
∴C(0,2),A(-4,0),
由抛物线的对称性可知:点A与点B关于x=-
对称,
∴点B的坐标为1,0).
②∵抛物线y=ax2+bx+c过A(-4,0),B(1,0),
∴可设抛物线解析式为y=a(x+4)(x-1),
又∵抛物线过点C(0,2),
∴2=-4a
∴a=-
∴y=-
x2-
x+2.
(2)设P(m,-
m2-
m+2).
过点P作PQ⊥x轴交AC于点Q,
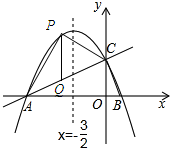
∴Q(m,
m+2),
∴PQ=-
m2-
m+2-(
m+2)
=-
m2-2m,
∵S△PAC=
×PQ×4,
=2PQ=-m2-4m=-(m+2)2+4,
∴当m=-2时,△PAC的面积有最大值是4,
此时P(-2,3).
| 1 |
| 2 |
∴C(0,2),A(-4,0),
由抛物线的对称性可知:点A与点B关于x=-
| 3 |
| 2 |
∴点B的坐标为1,0).
②∵抛物线y=ax2+bx+c过A(-4,0),B(1,0),
∴可设抛物线解析式为y=a(x+4)(x-1),
又∵抛物线过点C(0,2),
∴2=-4a
∴a=-
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)设P(m,-
| 1 |
| 2 |
| 3 |
| 2 |
过点P作PQ⊥x轴交AC于点Q,

∴Q(m,
| 1 |
| 2 |
∴PQ=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
∵S△PAC=
| 1 |
| 2 |
=2PQ=-m2-4m=-(m+2)2+4,
∴当m=-2时,△PAC的面积有最大值是4,
此时P(-2,3).
看了 如图,在平面直角坐标系xOy...的网友还看了以下:
一道中考题如下答案选C,解析:在上升阶段平均的升力为3N,我想问问初中学生怎么理解平均的升力为3N 2020-05-17 …
某同学探究溶液的酸碱性对FeCl3水解平衡的影响,实验方案如下:配制50mL0.001mol/LF 2020-05-17 …
关于一个溶解平衡的问题!例如:在Agcl的饱和溶液中存在着溶解平衡:Agcl(s)=(可逆)Ag( 2020-05-23 …
下列关于沉淀溶解的说法正确的是()A.只有难溶电解质才存在沉淀溶解平衡过程B.沉淀溶解平衡过程是可 2020-06-30 …
下列对沉淀溶解平衡的描述正确的是()A.反应开始时,溶液中各离子浓度相等B.沉淀溶解达到平衡时,沉 2020-07-26 …
难溶电解质与易溶电解质溶解平衡的区别为什么课本上会吧沉淀溶解平衡抽出来特别的讲啊?我想比如NaCl的 2020-11-08 …
下列关于沉淀溶解的说法正确的是[]A.只有难溶电解质才存在沉淀溶解平衡过程B.沉淀溶解平衡过程是可逆 2020-11-16 …
一道溶解平衡的题已知Ksp[Mg(OH)2]=1.8E-11,则Mg(OH)2在0.1mol/LMg 2020-12-19 …
下列对沉淀溶解平衡的描述正确的是()A.反应开始时,溶液中各离子浓度相等B.沉淀溶解达到平衡时,沉淀 2021-01-08 …
有关水解平衡的问题,氯化铵水解平衡后,再加水,为什么c(H)降低,c(OH)升高? 2021-02-01 …