早教吧作业答案频道 -->数学-->
如图,四边形ABCD是O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.(1)求∠OCA的度数;(2)若∠COB=3∠AOB,OC=23,求图中阴影部分面积(结果保留π和根号)
题目详情
如图,四边形ABCD是 O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.
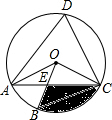
(1)求∠OCA的度数;
(2)若∠COB=3∠AOB,OC=2
,求图中阴影部分面积(结果保留π和根号)

(1)求∠OCA的度数;
(2)若∠COB=3∠AOB,OC=2
| 3 |
▼优质解答
答案和解析
(1)∵四边形ABCD是 O的内接四边形,
∴∠ABC+∠D=180°,
∵∠ABC=2∠D,
∴∠D+2∠D=180°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∵OA=OC,
∴∠OAC=∠OCA=30°;
(2)∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC-∠AOB=90°,
在Rt△OCE中,OC=2
,
∴OE=OC•tan∠OCE=2
•tan30°=2
×
=2,
∴S△OEC=
OE•OC=
×2×2
=2
,
∴S扇形OBC=
=3π,
∴S阴影=S扇形OBC-S△OEC=3π-2
.
∴∠ABC+∠D=180°,
∵∠ABC=2∠D,
∴∠D+2∠D=180°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∵OA=OC,
∴∠OAC=∠OCA=30°;
(2)∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC-∠AOB=90°,
在Rt△OCE中,OC=2
| 3 |
∴OE=OC•tan∠OCE=2
| 3 |
| 3 |
| ||
| 3 |
∴S△OEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S扇形OBC=
90π×(2
| ||
| 360 |
∴S阴影=S扇形OBC-S△OEC=3π-2
| 3 |
看了 如图,四边形ABCD是O的内...的网友还看了以下:
一个三角形的三个内角的度数比是3:2:1,这三个内角度数分别是()()().一个三角形的三个内角的 2020-05-19 …
模块的内聚是从功能的角度来度量模块内的联系,内聚度量的是()。A.通信内聚B.功能内聚C.顺序内聚D 2020-05-23 …
模块的内聚是从功能的角度来度量模块内的联系,内聚度最强的是()。A.通信内聚B.功能内聚C.顺序内聚 2020-05-23 …
物体以10m/S的初速度做匀加速运动前4S内的平均速度为18m/S求第四末的速度(2)物体加速度( 2020-06-02 …
换热器设计时管箱长度怎么计算的?按照GB151-1999中5.2.2的管箱的最小内侧深度指什么?最 2020-06-12 …
关于自由落体运动,下列说法正确的是()A.某段位移内的平均速度等于初速度与末速度和的一半B.某段时 2020-06-22 …
一物体沿直线运动,第一秒内速度为3m/s,第二秒内速度为2m/s,第三秒内速度为1m/s,第四秒内速 2020-12-09 …
冬天,我国一些城市实行水暖供热,户外温度为-5℃时,某房屋的室内温度为22℃;户外温度为-15℃时, 2020-12-10 …
如图所示是某物体运动的速度v随时间t变化的图像,由图像得到的正确结果是()A.0~2s内的平均速度是 2021-01-29 …
三角形的三内角和为180度,已知三角形的一个内角为(4x-10)度,另一个内角为(5X+10)度,第 2021-02-01 …